Aufgabe Winkelhaus:
Ein Winkelhaus hat die dargestellten Maße.
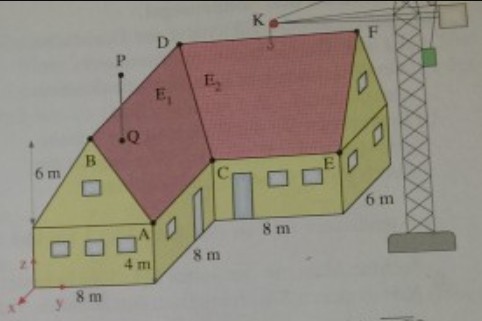
a) Bestimmen Sie die Koordinaten von \( \mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{E} \) und \( \mathrm{F} \).
b) Bestimmen Sie die Gleichungen der Firstgeraden \( \mathrm{g}_{\mathrm{BD}} \) und \( \mathrm{gFD} \). Hinweis: Die Richtungsvektoren sind einfach zu bestimmen.
c) Berechnen Sie den Punkt D als Schnittpunkt der Firstgeraden \( g_{B D} \) und \( g_{F D} \).
d) Wie lautet die Gleichung der Kehlgeraden \( g_{DC} \)? Wie lang ist die Dachkehle \( \overline{\mathrm{DC}} \) ?
e) Welchen Winkel bildet die Dachfläche \( \mathrm{E}_{2} \) zwischen der Kehle \( \overline{\mathrm{CD}} \) und der Traufe \( \overline{\mathrm{CE}} \) ?
f) Die Dachfläche \( \mathrm{E}_{2} \) soll komplett mit Solarzellen belegt werden. Wie groß ist die zu belegende Fläche? (Hinweis: Zerlegen Sie die Dachfläche in zwei Dreiecke und verwenden Sie die vektorielle Formel für den Flächeninhalt des Dreiecks.)
g) Die Spitze der abgebildeten Antenne hat die Koordinaten \( \mathrm{P}(-2|5| 12,5) \). In welchem Punkt \( Q \) durchstößt die Antenne die Dachfläche \( E_{1} \) ? (Hinweis: Stellen Sie zunächst die Gleichung der Ebene \( \mathrm{E}_{1} \) auf.)
h) Sonnenlicht in Richtung des Vektors \( \overrightarrow{\mathrm{v}}=\left(\begin{array}{r}-4 \\ 2 \\ -7\end{array}\right) \) erzeugt einen Schatten der Antenne auf der Dachfläche \( \mathrm{E}_{1} \). Berechnen Sie den Schattenpunkt \( \mathrm{P}^{\prime} \) der Antennenspitze \( \mathrm{P} \).
i) Die Auslegerspitze des Kranes hat die Koordinaten K(11|12|26). Von dort soll ein Seil zur Dachfläche \( \mathrm{E}_{2} \) gespannt werden. Wie lang muss das Seil mindestens sein?
