Hi!
Mir ist die Integralrechnung selbst noch nicht ganz vollständig erschlossen, dennoch bemühe ich mich einer Antwort.
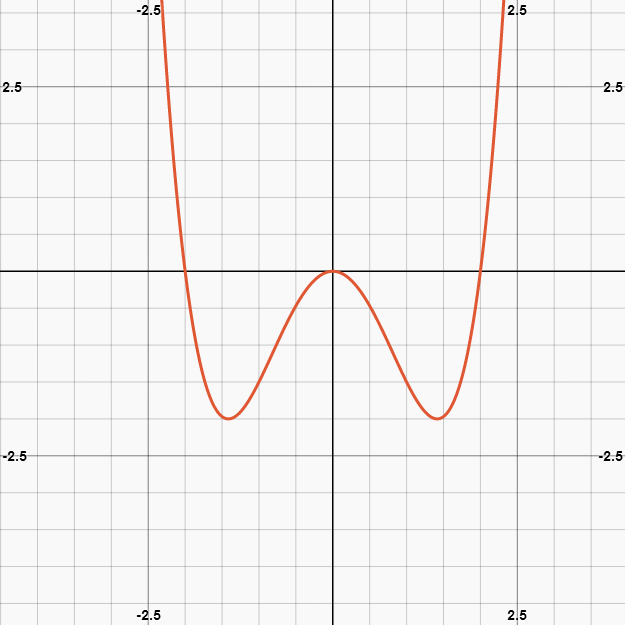
Die Intervallgrenzen liegen bei den Nullstellen, da die Fläche unter der x-Achse berechnet werden soll.
0,5x²(x²-4)=0
Die erste Nullstelle ist klar, (0|0), da das x vor der Klammer als Faktor reicht, um die gesamte Funktion = 0 zusetzen.
Für die nächsten beiden Nullstellen schauen wir uns die Klammer an.
(x²-4)= 0
x² = 4 |√
x = ±2
Also sind Nullstellen x 2 / 3 = (±2|0)
Nun bestimmen wir die Stammfunktion F(x)
Wir leiten auf, aus (x²(x²-4) / 2) wird (x4 - 4x2 ) /2 und aufgeleitet :
∫f(x) dx = F(x) = x³ * (0,1x² -2/3 ) + C
Nun je 2 und -2 für x einsetzen
F(a) - F(b) = [2³ * (0,1*2² -2/3 ) + C]- [(-2)³ * (0,1*(-2)² -2/3 ) + C]
= 2,133 +C - ( -2,1333 + C )
≈ 4,27
Gruß Luis