Was tun, wenn zwei Graphen mehrere Flächen unter- und über der x-Achse einschließen?

Question

Hallo,

wenn man zwei Graphen gegeben hat, die zusammen verschiedene Flächen einschließen, welche sowohl über also auch unter der x-Achse liegen und auf mehrere Quadranten verteilt sind, wie berechnet man diese Flächen dann?

Als Beispiel eine Zeichnung:

Wenn ich hier die Flächen ausrechnen wollte, die f und g mit der x-Achse einschließen, könnte ich dann einfach das Integral von -1,5 bis 3 nehmen und dann f von g abziehen, oder müsste ich jede Fläche einzeln berechnen?

Falls jemand eine gute Übungsaufgabe dazu hat, wäre das super.

Vielen Dank : )

Comments

Schraffiere doch einmal die gesuchte Fläche, damit deutlich wird, was genau berechnet werden soll.

Answer 1

Hallo,

ich würde die Flächen einzeln berechnen.

Folgende Aufgaben habe ich gefunden, die dir hoffentlich weiterhelfen:

2 Gegeben sind die Funktionen \( f \) und \( g \). Drücken Sie den Inhalt der beschriebenen Fläche mit \( A_{1}, A_{2}, A_{3} \ldots \) aus und berechnen Sie sie mit einem Integral.
Fläche I: Begrenzt vom Graphen von \( f \) und der \( x \)-Achse.
Fläche II: Begrenzt von den Graphen von \( f \) und \( g \).
Fläche III: Im 1. Quadranten begrenzt vom Graphen von f, der \( x \)-Achse und der \( y \)-Achse.
Fläche IV: Im 3. Quadranten begrenzt vom Graphen von f, der \( x \)-Achse und der Geraden \( x=-2 \).

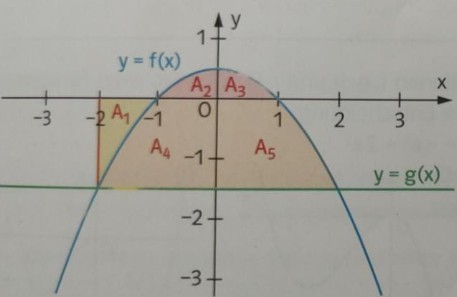
a) \( f(x)=-0,5 x^{2}+0,5 ; \quad g(x)=-1,5 \)

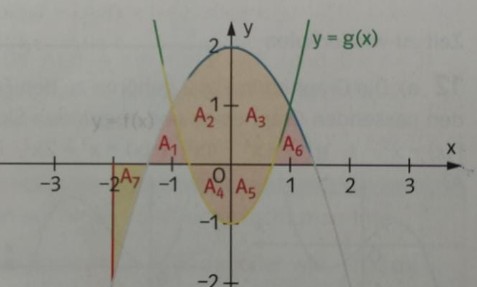
b) \( f(x)=-x^{2}+2 ; g(x)=2 x^{2}-1 \)

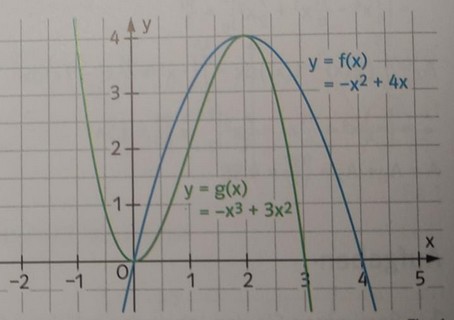
Berechnen Sie den beschriebenen Flächeninhalt in Fig. \( 1 . \)

a) Begrenzt von den Graphen von \( f \) und \( g \).
b) Begrenzt von den Graphen von \( f \) und \( g \) und der \( x \)-Achse.
c) Begrenzt vom Graphen von f, der \( y \)-Achse und der Geraden \( y=4 \).

Gruß, Silvia

Comments

Super, vielen Dank : )