Ich sah eben diese Aufgabe und habe mein Matheprogramm bemüht.
Ich gehe davon aus, das die Aufgabe 4 = (3 – e0,2x)2 die ursprüngliche Form ist.
Mein Matheprogramm hat für die entsprechende Funktion
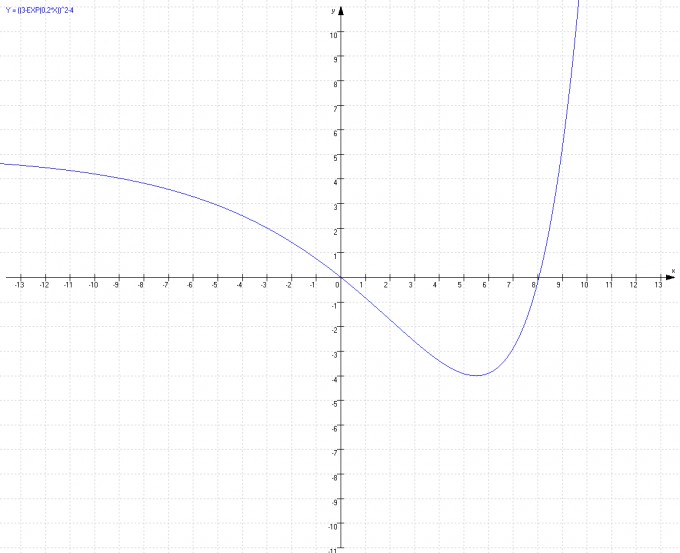
y = (3 – e0,2x)2 - 4
als Nullstellen x1 = 0 und x2 = 8,047 = 5ln5 angegeben, außerdem das Minimum (5,493;-4)
Wie man rechnerisch auf x2 kommt, weiß ich auch nicht.
Die Funktion sieht folgendermaßen aus.