Baumdiagramm und Mengendiagramm. Drei alte Gewehre stehen im Schrank.

Question

Die böse Aufgabe lautet:

Drei alte Gewere stehen in einem dunklen Kasten. Sie haben eine Trefferwahrscheinlichkeit von 65% 15% und 75%. Eines der Gewehre wird zufällig genommen. Eine Büchse ist das Ziel. Höchstens zwei Schüsse werden abgegeben. Mit welcher Wahrscheinlichkeit wird die Büchse getroffen?

Ich dank euch für einen schönen Rechenweg. :)

Answer 1

Ein Gewähr hat die trefferwahrscheinlichkeit p. Wie groß ist die Wahrscheinlichkeit bei 2 Schüssen mind 1 Treffer zu haben.

P = (1 - (1 - p)^2)

Wir haben hier also die Wahrscheinlichkeit

P = 1/3 * (1 - (1 - 0.65)^2) + 1/3 * (1 - (1 - 0.15)^2) + 1/3 * (1 - (1 - 0.75)^2) = 69.75%

Answer 2

\( p(T) = 1-(289/1200+49/1200+1/48) = 279/400 \)

Answer 3

Das ist ja wohl so:

Erst wirst ein Gewehr ausgewählt , für jedes p=1/3.

Dann wird damit geschossen:

Bei Treffer ist Schluss, bei Niete wird nochmal geschossen.

Mein Baum sähe so aus:

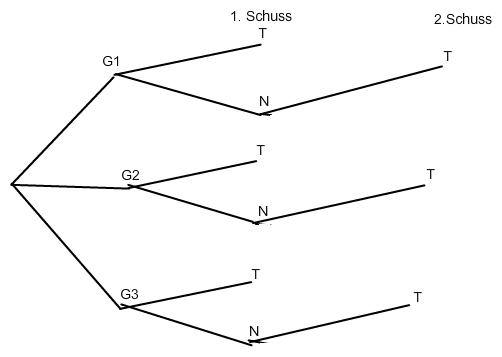
Es gibt also 6 Pfade zu dem gewünschten Ergebnis: "Büchse getroffen"

von oben nach unten wäre das

(1/3) * 0,65    +

(1/3)*0,35*0,65  +

(1/3) * 0,15   +

(1/3) * 0,85 * 0,15 +

(1/3) * 0,75  +

(1/3) * 0,25 * 0,75      =  279/400 = 69,75%