Sei x≠ -1
f(x)= (x2 -1)/ (x+1)
f(x) = ((x -1)(x+1)) / (x+1) =
f(x) = x-1 , überall, wo x≠-1
x gegen + unendlich: (x-1) → unendlich
x gegen - unendlich: (x-1) → - unendlich
Nun zur Definitionslücke:
[ lim x--> -1links x] (x-1)
EPSILON>0 gegen 0
=lim ( -1-EPSILON - 1) =lim (-EPSILON-2) → -2
[ lim x--> -1lrechts x] (x-1)
EPSILON>0 gegen 0
=lim ( -1+EPSILON - 1) =lim (EPSILON) → -2
Nun musst du das aber noch in eurer gewohnten Schreibweise aufschreiben.
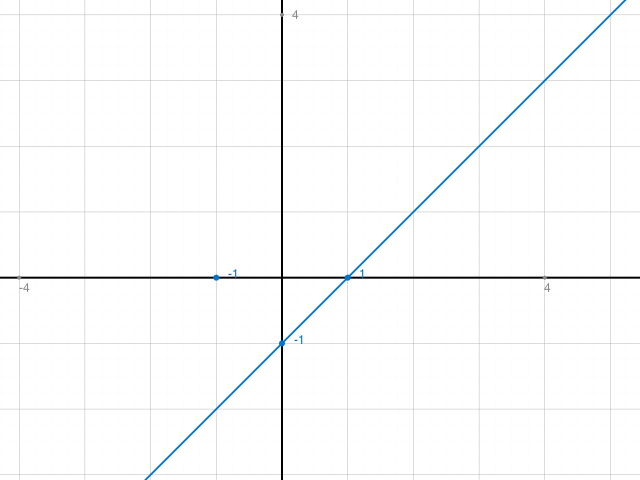
Im Graphen sieht man das 'Loch' bei (-1,-2) gar nicht. Der Punkt bei (-1|0) ist am falschen Ort, weist aber darauf hin, dass die Rechnung dem Plotter dort ein Problem bereitete.