Ein zur y-Achse paralleler Streifen der Breite b = 2 wandert auf der x-Achse
entlang und bestimmt damit ein Parabelsegment für die gegebene
Normalparabel f(x) = x2. Für welchen Streifen ist die Fläche des Segments
maximal?
Hilfe: die Fläche innerhalb des Streifens und unterhalb der Parabel berechnet
sich nach A= 1/3(z+2)³- 1/3z³, wobei z ein beliebiger Anfangswert (x-Wert) des
Streifens ist und der Streifen dann bei z+2 endet.
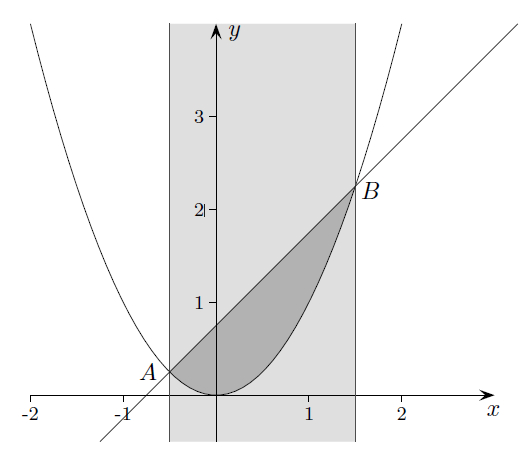
Die Funktion, die in der Hilfe angegeben ist berechnet ja die dunkle Fläche und die darunter, jedoch möchte man, dass nur die dunkle Fläche maximal wird. Heißt das jetzt, dass ich das Integral von x^2 zusätzlich abziehen muss, wenn ich die Grenzen habe? Weil das sollte doch schon - 1/3z³ machen oder nicht?
Meine Idee war jetzt die die erste Ableitung der Funktion oben Null zu setzen. Dann kommt man auf z=-1. Aber was mache ich jetzt?