Schon allein weil oben von wöchentlich gesprochen wird und dann hat
man aber Tageskapazitäten. Bin total verwirrt.
x = Produktionstage der 1.Bäckerei
y = Produktionstage der 2.Bäckerei
Wöchentlich nimmt das Krankenhaus 1200 kg Brötchen ab.
x * 600 + y * 200 = 1200
Deine Nebenbedingungen
600x + 200y = 1200
400x + 1200y = 2400
200x + 200y = 800
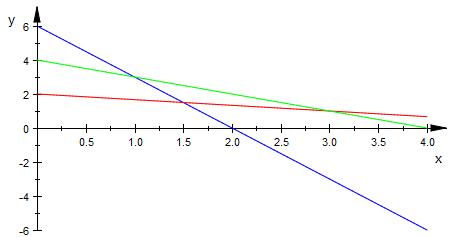
Da wir nicht wissen ob es eine optimale Lösung gibt sind dies die
Mindestmengen die produziert werden müssen.
Also gilt für die Nebenbedingungen
600x + 200y ≥ 1200
400x + 1200y ≥ 2400
200x + 200y ≥ 800
Alles oberhalb der Teilgeraden von blau,grün,rot erfüllt die Bedingungen.
Zielfunktion
2000 * x + 1600 * y = Kosten
y = Kosten / 1600 - 2000/1600 * x
y = Kosten / 1600 - 1.25 * x
Die Zielfunktion ( Gerade ) hat die Steigung - 1.25.
Du zeichnest jetzt oberhalb von blau,grün und rot eine Gerade mit
der Steigung -1.25 ein.
Dann verschiebst du die Gerade nach unten bis zum tiefstmöglichen Punkt
im Zielbereich.
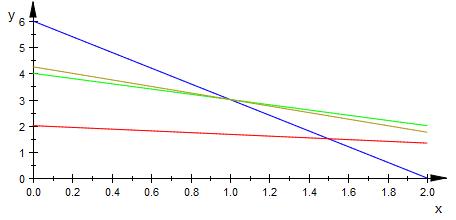
Der tiefstmögliche Punkt ist ( 1 | 3 ).
Dieser ist gleich blau, gleich grün und oberhalb von rot.
Der y-Achsenabschnitt ist geschätzt 4.25.
Nach obiger Formel
y = Kosten / 1600 - 1.25 * x
Kosten / 1600 = 4.25 betragen die minmalen wöchentlichen Kosten
6800 €
( 1 | 3 ) eingesetzt in die Zielfunktion
2000 * 1 + 3 * 1600 = 6800.
Das Ergebnis hat sich bestätigt.