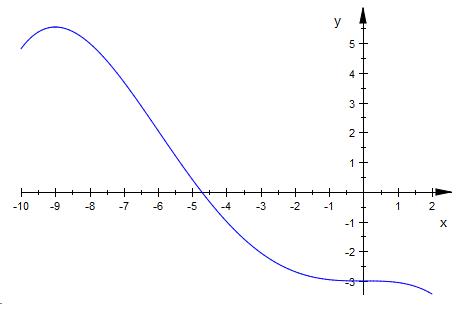
f ( x ) = - 1/256 * ( x + 4 * t ) * x^3 - t
f3 ( x ) = - 1/256 * ( x + 4 * 3 ) * x^3 - 3
f3 ( x ) = - 1/256 * ( x + 12 ) * x^3 - 3
f3 ( x ) = - 1/256 * ( x^4 + 12 * x^3 ) - 3
f3 ´( x ) = -1/256 * ( 4 * x^3 + 36 * x^2 )
Stellen mit waagerechter Tangente
( 4 * x^3 + 36 * x^2 ) = 0
x^2 * ( 4 * x + 36 ) = 0
Satz vom Nullprodukt
x^2 = 0
x = 0
und
4 * x + 36 = 0
x = -9
f3 ´´ ( x ) = -1/256 * ( 12 * x^2 + 72 * x )
f3 ´´ ( 0 ) = -1/256 * ( 12 * 0 + 72 * 0 ) = 0
f3 ´´ ( -9 ) = -1/256 * ( 12 * (-9)^2 + 72 * (-9) ) =-1.26 ( Hochpunkt )
Monotonie > 0
-1/256 * ( 4 * x^3 + 36 * x^2 )
4 * x^3 + 36 * x^2 < 0
x^2 * ( 4 * x + 36 ) < 0
x^2 ist stehts > 0
4 * x + 36 < 0
x < -9
bei x = 0 findet kein Wechsel der Monotonie statt.
x = 0 ist kein Extrempunkt.