Aufgabe:
Ein Ölfeld wird seit Beginn des Jahres 1990 mit Bohrungen in mehreren Erdöl führenden Schichten erschlossen. Die momentane Förderrate aus diesem Ölfeld im Zeitraum von Anfang 1990 bis Ende 2009 kann im Intervall [0;20] durch die Funktion \( f \) mit der Gleichung
\( f(t)=(1.020-40 t) \cdot \mathrm{e}^{\frac{1}{10} t}, t \in \mathbb{R} \)
modelliert werden.
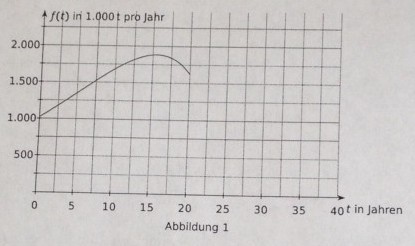
Dabei wird \( t \) als Maßzahl zur Einheit 1 Jahr und \( f(t) \) als Maßzahl zur Einheit \( 1.000 \) Tonnen pro Jahr aufgefasst. Der Zeitpunkt \( t=0 \) entspricht dem Beginn des Jahres 1990 . Der Graph von \( f \) ist in der Abbildung 1 in dem für die Modellierung zu betrachtenden Intervall dargestellt.
a)
1. Bestimmen Sie den Zeitpunkt im betrachteten Zeitraum von Anfang 1990 bis Ende 2009, zu dem die Förderrate maximal ist, und berechnen Sie den Maximalwert. [Zur Kontrolle: \( \left.f^{\prime}(t)=(62-4 t) \cdot \mathrm{e}^{\frac{1}{10} \cdot t}\right] \)
2. Zeigen Sie, dass die Förderrate im Zeitraum von Mitte 2005 bis Ende 2009 ständig zurückgeht und der Rückgang dabei immer stärker wird.
b)
Die Menge des Erdöls, das seit dem Beginn der Ölförderung Anfang 1990 bis zu einem beliebigem Zeitpunkt \( t \) des betrachteten Zeitraums aus dem Ölfeld gefördert wurde, wird durch eine Funktion \( M: t \mapsto M(t), 0 \leq t \leq 20 \), beschrieben.
1. Bestimmen Sie eine Gleichung dieser Funktion \( M \).
2. Berechnen Sie die gesamte Fördermenge aus dem Ölfeld von Anfang 1990 bis Ende 2009.