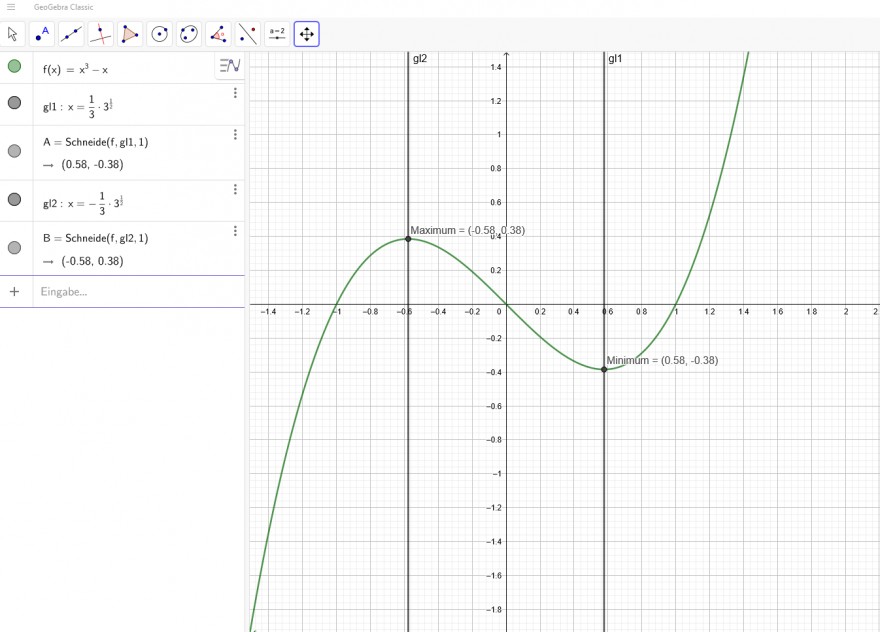
f1(x)= x^3 -x
Nullstellen:
x^3 -x=0
x(x^2-1)=0
x₁=0 x₂=1 x₃ =-1
Extremwerte:
f´(x)= 3x^2 - 1
3x^2 - 1=0
x₁= 1/3* \( \sqrt{3} \) →f(x₁)= ...
x₂= -1/3* \( \sqrt{3} \) →f(x₂)= ...
Art des Extremwertes:
f´´(x)= 6 x
f´´(x₁)= 6 x₁ > 0 → Minimum
f´´(x₂)= 6 x₂ < 0 → Maximum
Wendepunkt:
f´´(x)=0
x=0 → y= 0 Punktsymmetrie im Ursprung.
mfG
Moliets