Grenzwert 1/x + ln(x) für x gegen 0+

Question

Hi,
weiß jemand, ob mein Lösungsweg korrekt ist?

$$ \lim \limits_{ x\to 0^+ }{ \left(\frac { 1 }{ x } +\ln { (x) } \right) } \\ =\lim \limits_{ z\to \infty  }{ \left(\frac { 1 }{ 1/z } +\ln { (1/z) } \right) } \\ =\lim\limits_{ z\to \infty  }{ (z+\ln { (1/z) } ) } \xrightarrow{z\to\infty} \infty $$

Hat jemand eventuell noch einen Tipp, wie man Grenzwerte, wo x gegen ≠ ∞ geht, lösen kann?
L-Hospital und wie ich es gemacht habe mit der Substitution  fallen mir nur ein. Falls kein linksseitiger/rechtsseitiger Grenzwert gesucht ist (sondern z.B. nur x -> 0) dann könnte man doch auch den linksseitigen + rechtsseitigen Grenzwert berechnen und schauen ob diese übereinstimmen?

Danke, Gruß

Comments

Ich weiß nicht wie du auf dein Ergebnis in der letzten Zeile
gekommen bist.

lim z −> ∞  [ z + ln ( 1 / z ) ] = [ z + ln ( 0+ ) ] = ∞ - ∞ = ?

---

Dachte weil z schneller wächst als ln(z) , somit immer z > ln(z)

---

Vielleicht so$$z-\log z=\log\frac{e^z}z>\log\frac{1+z+\frac{z^2}2}z=\log\left(\frac1z+1+\frac z2\right)\xrightarrow{z\to\infty}\infty.$$

---

@Fragesteller
Also so
lim z −> ∞  [ z + ln ( 1 / z ) ] = [ z + ln ( 1 )  - ln ( z ) ] = [ z - ln ( z ) ]
Mit dem Wissen z > ln ( z ) wäre der Beweis erbracht.

Ansonsten ist mir mit etwas Umformerei der Beweis
über l ´Hospital auch gelungen.

Weißt du wo ich irgendwo eine Aufstellung finde wie sich die Standard-Funktionen
x, x^2 , Wurzel (x ), ln ( x ),2^x  untereinander bei Grenzwerten verhalten
also x > ln(x) usw.

---

Welcher Beweis wäre mit dem Wissen z > ln ( z ) erbracht?

---

Keiner. Stimmt.
Ich stelle jetzt einmal den Beweis mit l´Hospital ein.

Answer 1

$$\ln(\frac 1z)=- \ln(z)$$

Answer 2

Hier der Nachweis über l ´Hospital

Comments

Was hast Du denn unter der ersten grünen Linie gemacht?

---

Im Zähler des Bruchs steht der Ausdruck x * ln ( x ).

Für diesen habe ich mir einmal angeschaut was passiert bei
lim x −> 0(+)  [ x * ln ( x ) ] −> 0 * ( -∞ )
0 * ( -∞ ) ist noch nicht klar.

Dann  habe ich umgeformt
x * ln ( x ) = ln ( x ) / ( 1 / x ) .
Bei lim x −> 0(+) entspricht dies : -∞ / ∞.

Dafür kann l´Hospital angewendet werden.

lim x −> 0(+)  [ x * ln ( x ) ] −> -x

---

Du ersetzt also \(\pmb{x\cdot\ln x}\) durch \(\pmb{-x}\) ?

---

Oh. Du hast aber noch gute Augen.
Wo ist dein Problem ?

---

$$\large\lim_{x\to0}\ln x=\lim_{x\to0}\frac{\pmb{x\cdot\ln x}}x\overset?=\lim_{x\to0}\frac{\pmb{-x}}x=\lim_{x\to0}(-1)=-1.$$Kann das sein?

---

Die Angelegenheit ist verzwickt, ich meine dein Fehler liegt zwischen
dem 2 und 3 Schritt.

2.Schritt : akzeptiert
Gilt der 3.Schritt für den Zähler nur falls x −> 0(+)  bereits gegangen ist ?
Dann müßte auch für den Nenner gelten : 0
-x / 0 = - ∞

Vielleicht bei mir auch nicht ganz richtig. Unter der letzten grünen Linie
müßte stehen
lim x −> 0(+)  [ ( 1 + x * ln ( x ) ) / x ] −> [ ( 1 + ( -0 ) ) / 0 ] −> 1 / 0 −> ∞

Ich will jetzt fernsehen. Außerdem muß ich mir Lu´s Anwort auch noch
ansehen.

---

Das ist nicht mein Fehler, sondern deiner.

---

3 deiner Kommentare sind nur Einzeiler. Das ist ein bißchen dürftig.

Teile mir doch mit wo bei mir ein Fehler vorliegt.
Dann haben wirs hinter uns.

---

Ich denke ich gehe bei l´Hospital noch weiter zu 0

Dann ergibt sich für die Frage und auch dein Beispiel
der richtige Wert

---

Teile mir doch mit wo bei mir ein Fehler vorliegt.
Das habe ich bereits getan.

---

Da du ja nur kryptsche Einzeiler hier einstellst die mich nicht
weiterbringen teile ich dir ein letztes Mal mit wo meiner Meinung
nach dein Fehler liegt.

In deinem 3.Schritt ersetzt du den Zähler mit meiner Lösung für
lim x −> 0(+)  [ x * ln ( x ) ] −> -x
dies gilt nur für  lim x −> 0(+) .

Dann hättest du in diesem Schritt auch den Nenner ersetzen müssen
lim x −> 0(+)  [ x ] −> -0

Das war mein letzter Kommentar. Ich habe besseres zu tun.
Auf deine Meinung lege ich keinen Wert mehr.

---

Das ist auch nicht meine Intention.

---

Es interessiert mich etwas :
Was sind den deine Intentionen. Eitle Selbstdarstellung ?

---

Nein,derartiges sei dir überlassen.

---

L'Hopital ist ein Satz zur Berechnung von Grenzwerten, nicht von einseitigen Grenzwerten.

Der Satz ist hier nicht anwendbar.

---

Sorry, mein obiger Kommentar (den ich nicht mehr editieren kann) ist Bullshit.

Es gibt eine Variante von L'Hopital die auf einseitige Grenzwerte angewendet werden kann und die Voraussetzungen sind hier erfüllt., also bei der Anwendeung auf xln(x).

(auf den ursprünglichen Term geht es nicht.)

Bei der Rechnung - so wie ich sie verstehe - funktioniert aber meines Erachtens so nicht, da scheinbar \( lim_x \frac{1+f(x)}{x} = \lim_x \frac{1 +\lim_x f(x)}{x}\) verwendet wird,

Diese Regel gibt es aber nicht, z.B. $$ \lim_{x \to 0} \frac{1+x}{x} = \lim_{x \to 0}(\frac{1}{x}+1) =1 $$

Aber $$\lim_{x \to 0}\frac{1+\lim_{x \to 0} x}{x}=\lim_{x \to 0}\frac{1+0}{x}  =\infty $$.

Und georgborn ich finde deine Reaktion auf die Nachfrage sehr pampig und unfreundlich.

---

@Gast

Das ist auch nicht meine Intention.

Dann wiederhole ich meine Frage ( die du ja noch nicht beantwortet hast ) :

Es interessiert mich etwas :
Was sind den deine Intentionen ?

Mit der Bitte um eine klare Antwort.

---

@tatmas
Und georgborn ich finde deine Reaktion auf die
Nachfrage sehr pampig und unfreundlich

Ich nehme das zunächst einmal zur Kenntnis.
Ich sehe die Angelegenheit aber genau umgekehrt..

Dein Beispiel verstehe ich nicht ( 1.Berechnung )
lim x −> 0 (+)  [ ( 1 + x ) / x ]
lim x −> 0 (+)  [ 1 / x + x / x ]
da wir ja noch vor x = 0 sind darf gekürzt werden x / x = 1
lim x −> 0 (+)  [ 1 / x + 1 ] −> ∞ + 1 −> ∞

Ich würde aber gern über meinen letzten handschriftlichen
Beitrag reden, da ich gern wüßte wo dort mein ( vermeintlicher )
Fehler liegt

Was ist falsch
lim x  −> 0 (+)  [ x * ln ( x ) ] = ?

Hier der Graph ( ohne L´Hospital ]

~plot~ x * ln ( x ) ~plot~

Mir scheint
lim x  −> 0 (+)  [ x * ln ( x ) ] = 0

---

Ein anderes Beispiel:

$$\lim_{x \to 0} \frac{1+(-1+x)}{x} =\lim_{x \to 0} \frac{x}{x}=1$$,

aber

$$\lim_{x \to 0} \frac{1+\lim_{x \to 0}(-1+x)}{x} =\lim_{x \to 0} \frac{1-1}{x}=\lim_{x\to 0} \frac{0}{x} =\lim_{x \to 0} 0 =0$$,

---

Ich meine du machst den Fehler den du mir vorwirfst
nämlich lim x −> 0 zeitlich nacheinander auf Teilterme
anzuwenden

lim x −> 0  [ ( 1 + ( -1 + x ) ) /  x ]

Jetzt lim x −> 0 auf ALLES anwenden. Im ersten Schritt.

( lim x −> 0  ( 1 ) + lim x −> 0  ( -1 + x ) )  /  lim x −> 0  ( x )

( 1 + (-1) ) / 0 = 0 / 0 : Ab jetzt wieder ein Fall für l ´Hospital

[ 1 + ( -1 + x ) ] ´ /  x ´ = 1 / 1 = 1

Damit wir einmal wieder auf  die Frage des Fragestellers zurückkommen

lim x  −> 0 (+)  [ x * ln ( x ) ] = 0

die Aussage stimmt doch ? Oder?
( Dies ist eine Nebenrechnung für die nachfolgende Rechnung )

Die Aussage angewendet auf die Frage des Fragestellers

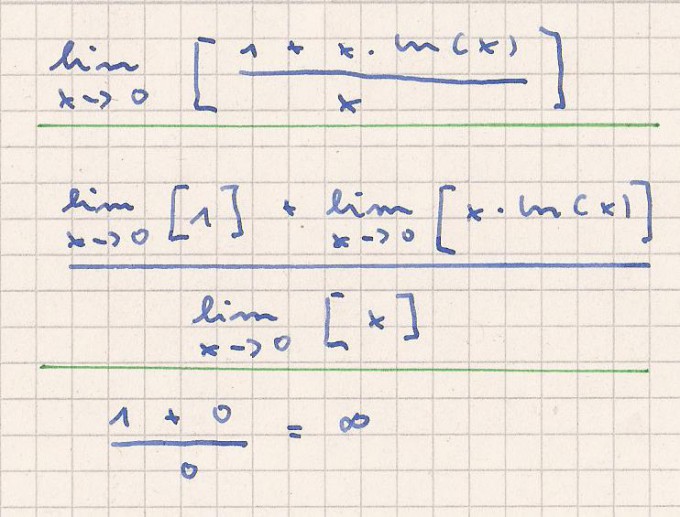
So sehe ich die Angelegenheit.

---

Lieber goergborn,

ich werfe dir keinen Fehler vor.  Einen Fehler zu machen ist auch nichts Schlimmes, passiert jedem.

Du scheinst das aber als persönlichen Angriff zu werten. Das ist es nicht.

( Fast alle mir bekannten Mathematiker freuen sich wenn man sie auf Fehler hinweist. Ist das hier eventuell ein Kulturclash?)

Zu meinem vorigen Post: 

Das war ein Gegenbeispiel,d.h. ein Beispiel das zeigt, dass die Aussage falsch ist.

Ja, \(lim_{x \to 0^+} x ln x=0 \).

Und deine weitere Rechnung kann ich nicht nachvollziehen, mit welcher Begründung machst du insbesondere den ersten Rechenschritt?

---

In meinem ersten Schritt wende ich den lim auf alle Teilterme an.

Beispiel
lim x −> 0 [ x^2 + 4 * x + 7 ]
lim x −> 0 [ x^2 ] + lim x −> 0 [ 4 * x ] + lim x −> 0 [ 7 ]

Das habe ich jetzt aber schon ein paarmal erklärt.

---

Vielleicht ist der Strang hier schon zu unübersichtlich, aber ich sehe nirgendwo, dass du erklärt hättest, dass du den Limes auf alle Teilterme anwendest.

Aber danke, jetzt ist es geklärt.

Der Schritt ist falsch.

https://de.wikipedia.org/wiki/Grenzwert_(Funktion)#Grenzwerts.C3.A4tze

So wie im letzten Post ist es möglich, weil die Voraussetzungen erfüllt sind.

So wie in deinem letzten handgeschrieben Post ist es nicht möglich, weil der Limes im Nenner Null ist und daher der entsprechende Grenzwertsatz (wie es auch im Wiki-Artikel) nicht in dieser Form angewendet werden kann.

(Oder verwendest du  einen anderen Satz bzw. eine andere Variante des Satzes?)

---

Leider verstehe ich den Wiki-Artikel komplett nicht.

In meinem handgeschrieben Beitrag gehe ich doch von Teil 1 nach Teil 2
genauso vor wie man im Kopf vorgehen würde.

Ich schaue mir einmal an was ich unter Grenzwertsätze finde.

---

Die Recherche brachte mich nicht weiter.

Offensichtlich gelingt es mir nicht dich zu überzeugen.
Umgekehrt ist es genauso.

Warum ist mein Ergebnis eigentlich richtig ?

---

Lieber georgborn,deine letzten beiden Posts lassen mich entsetzt zurück.
Es ist keine mathematische Begründung, dass das Vorgehen das ist wie in deinem (oder irgendjemades anderen) Kopf(es) ist. Schritte erfolgen nach mathematischen Regeln, hier den Grenzwertsätzen.Und wenn du nicht wirklich verstehst was du machst, da du ja anscheinend die Grenzwertsätze nicht kennst,ist es nicht naheliegend, dass du es falsch machst.(auch wenn du es bei den Standardfällen eventuell richtig machst. Das ist hier aber kein Standardfall)
Und deine letzte Frage ist hoffentlich nicht ernstgemeint. Natürlich kann man trotz Fehlern aufs richtige Ergebnis kommen, trotzdem ist das Vorgehen falsch.

---

ich (der Fragesteller) poste mal die Lösung für die die es interessiert ... Diese ist 100% richtig. Und nein die Vorposts/Kommentare waren nicht von mir, hat irgendein anderer Gast dazwischen gefunkt...

---

Hier ein letzter Versuch. Ein mir bekannter Lehrer hätte dem ersten
Term an der Tafel die roten Zusätze des zweiten Terms hinzugefügt.

Die ganze Angelegenheit ist doch völlig klar. Wo ist dort ein
Fehler ?

---

@Gast
Dann wiederhole ich meine Frage ( die du ja noch nicht beantwortet hast ) :
Es interessiert mich etwas :
Was sind den deine Intentionen ?
Mit der Bitte um eine klare Antwort.

@tatmas
Was ist deine Meinung zu meinem letzten Beitrag ?

Answer 3

1. Methode

z + ln( 1/z)         | Wie pleindespoir schon schrieb.

= z - ln(z)

Wenn man nun weiss, dass jede Potenz für genügend grosse z den Logarithmus schlägt, ergibt sich.

-------> ∞ für z gegen unendlich

und dein Weg wäre korrekt.

Allenfalls Rechnung von im 3. Kommentar zur Frage anfügen.

2. Methode mit Hospital mE fraglich

lim ( (1 + xln(x))/x)           | Problem: Im Zähler steht doch nicht "fast 0."

= lim ((0 + x*(1/x) + 1*ln(x)) / 1

= lim (1 + ln(x)) ---( limes _{x gegen 0+})---> - ∞   . Hier sieht man wohl, dass Hospital so nicht geht.