Gegeben sind 4 Gleichungen
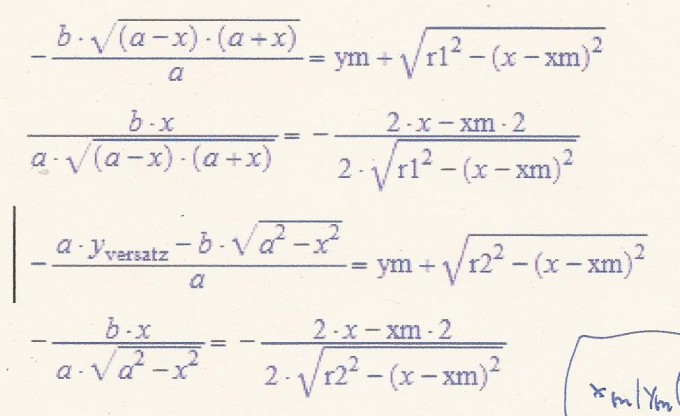
Bekannt sind a,b, r1, r2, y_versatz
Gesucht werden : xm, ym
Vorschlag zur Vorgehensweise
1.Gleichung nach x umstellen
x in die 2.Gleichung einsetzen
3.Gleichung nach x umstellen
x in die 4.Gleichung einsetzen
Es entstehen 2 Gleichungen mit den Unbekannten xm, ym
Diese dann entsprechend umstellen
Wer kanns zu Fuß oder mit einem Matheprogramm lösen ?