Berechnung des Volumens einer Fläche die um die x-Achse rotiert

Question

Die Fläche, die der Graph der Funktion h mit der Gleichung h(x)=2e^x mit den beiden Koordinatenachsen und der Gerade mit der Gleichung x=1/2ln5 einschließt, erzeugt bei Rotation um die x-Achse einen Körper. Prüfen Sie rechnerisch, ob das Volumen dieses Körpers größer als 20 VE ist.

Ich weiß, dass die Formel um das Volumen eines Rotierenden Körpers um die x-achse wie folgt aussieht:

V=π*∫(f(x))^2 dx  (obergrenze b untergrenze a)

Aber zum einen habe ich ja zwei Funktionen und nicht nur eine und zum anderen hat die funktion f ja überhaupt keine Nullstelle welche Grenzen soll ich denn da nehemen?

Comments

Die Funktion
h ( x ) = 2e^x

Hat als Fläche an der Stelle x
A ( x ) = [ h ( x ) ]^2 * π
A ( x ) =[ 2e^x ]^2 * π
A ( x ) = 4 * e^{2x} * π

Die Stammfunktion ist
∫ A ( x ) dx
∫  4 * e^{2x} * π dx
4 * π ∫  e^{2x}  dx
4 * π * 1/2 e^{2x} 
2 * π * e^{2x}

Integrationsanfang x = 0
Integrationsende x =1/2* ln(5) = 0.8047
V = [ 2 * π * e^{2x} ] ₀ ^{1/2* ln(5)}

V = 25.13

Bei Fragen wieder melden.

Answer 1

zuerst rechnest du dir die Schnittstellen aus.

Hier der Graph:

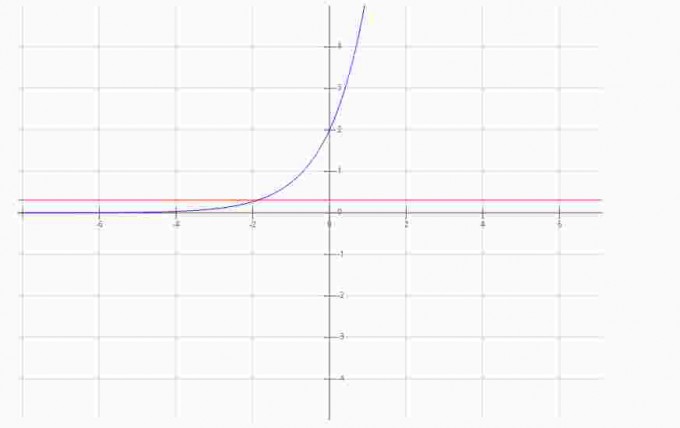
Das heißt du stellst beide Funktionsgleichungen gleich (also f(x) = g(x)).

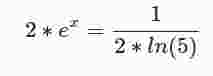
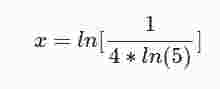
Es befindet sich eine Schnittstelle bei S₀(-1,862 | 0,31).

Wir drehen unsere Funktion um die X-Achse somit grenzen wir die Funktion an der Schnittstelle (untere Grenze) und dem Koordinatenursprung (obere Grenze) ein.

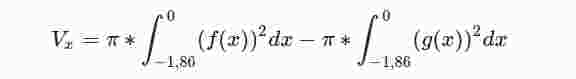
Einsetzen, integrieren und ausrechnen. Am Ende überprüfst du ob das Volumen > 20 VE ist.

Nicht vergessen den Betrag des Ergebnis zu nehmen.

Comments

Kleiner Hinweis von mir. die Gerade lautet x=... nicht y=...

Bitte Lösung überarbeiten.

---

Wow ist ja doch nicht so schwer wie gedacht! Danke für die Hilfe und die top Erklärung!

---

Werter Fragender, hast du auch gemerkt, das die Zeichnung und Rechnung nicht korrekt sind?

---

Außer das mit dem y=... nein, wo soll der Fehler liegen?
Bei der Umformung von g(x) war ich etwas verwundert.. aber ich habs nicht so mit ln..

---

Die Grenzen sind im Aufgabentext gegeben. beide Koordinatenachsen x-Achse, y- Achse und die Funktion h(x)=2e^x sowie die Gerade x=1/2ln(5).

---

Wie hast du g(x) umgeformt um sie so zu Zeichnen? 

---

Was ist g(x)? Ist im Aufgabentext nicht gegeben! Oder meinst du die Gerade x=1/2ln(5) ?

---

Naja schon, aber Normalerweise ist es doch immer in der Grundform y=mx+n.. wenn man damit jetzt rechnen will (oder irgendwo einzeichnen lassen will) müsste man hier erst nach y umstellen bzw. die Funktion umformen..

Ich kenn mich mit Ln-Funk.nicht mehr so gut aus, kann man das x einfach rüber holen.. also:

g(x)=y=1/2*ln(5) -x

??

---

Das Endresultat:

$$\pi \int_0^{\frac{1}{2}{ln(5)}}(2 e^x)^2 dx=8\pi\approx 25,133$$

https://www.wolframalpha.com/input/?i=pi*%5Cint_0%5E1%2F2ln%285%29+%282e%5Ex%29%5E2+dx

g(x)= 1/2ln(5) ist eine Funktion. x=1/2ln(5) ist eine vertikale Gerade aber keine Funktion.

---

ahhhhhh verstehe jetzt macht auch alles andere Sinn!!!

Ein Großes Danke @Sigma ich war am verzweifeln, da hätte ich auch früher drauf kommen können :D

Du warst meine Rettung

---

Bitte Und immer Alles Hinterfragen.

Hier noch die Lösung von Kalidhor. Ich hoffe er äußert sich noch. Ansonsten such dir einen Lösungsvorschlag von uns beiden aus.

https://www.wolframalpha.com/input/?i=%5Cpi*%5Cint_%7B-1.86%7D%5E0+%282e%5E%7Bx%7D%29%5E2+dx-%5Cpi+%5Cint_%7B-1.86%7D%5E0+%281%2F2+Ln%5B5%5D%29%5E2+dx

---

Beides klingt meiner Meinung nach plausibel, aber ich hatte überhaupt nicht dran gedacht, dass dies eine vertikale Gerade sein kann und das scheint mir dann doch logischer!

Schönen Abend noch und nochmal Danke :))

---

@sigma könntest du Rechenweg aufschreiben wie man die beiden Grenzwerte einsetzt und auf das Ergebnis kommt?

Also Rechenweg ohne, dass man zwangsweise ein Taschenrechner benutzt..

---

Es tut mir leid, dass ich Dich auf eine falsche Fährte gebracht habe. Mir ist erst beim zweiten Blick klar geworden, dass die Funktionsgleichung mit x und nicht y angeschrieben wurde. In diesem Fall wäre es eine einfache Parallele zur y-Achse und somit eine (obere) Grenze. Es war ein blöder Fehler von mir.

Immerhin ist Dir jetzt bekannt was zu machen ist, falls ein Schnittpunkt berechnet werden muss und mehrere Funktionen gegeben sind.

Ich entschuldige mich für dieses Ungeschick.

,

Kalidhor