Defekt einer Matrix mittels Rangsatz

Question

Ich hab eine Frage bezüglich der Berechnung des Defekts einer Matrix

Im Fall der Matrix

 

Diese wird nun in ZSF umgwandelt um ihren Rang bestimmen zu können:

 

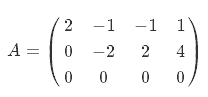
Der Rang ist nun die Anzahl der Zeilen ungleich 0, also 2.

Der Rangsatz def(A)= dim(A) - rang(A)

Nun meine Frage: Ich weiß, dass die Dimension einer Matrix der Anzahl ihrer Spalten entspricht.          
Bezieht sich die Dimension auf die "Ursprungsmatrix" oder die in ZSF? Oder ist das egal?

Wenn sich die Dimension nur auf die ZSF-Matrix bezieht und es eine Nullspalte geben würde (a11 wäre 0 statt 2), würde diese Nullspalte mit in die Dimension einbezogen werden oder wäre dann dim=3?

Answer 1

Nun meine Frage: Ich weiß, dass die Dimension einer Matrix der Anzahl ihrer Spalten entspricht.           
Bezieht sich die Dimension auf die "Ursprungsmatrix" oder die in ZSF? Oder ist das egal?

Gegenfrage ist die Anzahl der Spalten in der Ursprungsmatrix eine andere als in der ZSF? Ich denke nicht. Also ist das egal.

http://www.mathebibel.de/rangsatz

Comments

Im vorliegenden Fall war mir das Ergebins klar, das war eher eine theoretische Frage.
Wie wäre es denn mit meinem theoretischen Fall, also einer Nullspalte in der ZSF? Zählt die Nullspalte dann zur Dimension?

---

Ja. Es interessirt die Anzahl an Spalten und nicht die Anzahl von Null verschiedenen Nullspalten.

---

Vielen Dank für die konkrete Antwort.
Im Grunde kann man also sagen, dass sich die Dimension einer Matrix (bei Anwendung von Gauß) nie verändert.