Nullstellen der Funktion f(x)=x^3 - 3x +1 bestimmen

Question

ich habe mal eine kurze Frage. Mir ist in einem Skript gerade eine Polynomfunktion ins Auge gesprungen von der ich mal die Nullstellen bestimmen wollte. Leider gelingt mir das auf Anhieb nicht, da man auch keine so einfach erraten kann um den Linearfaktor abzuspalten.

Wie auch immer, die Funktion lautet;

f(x)=x^3 - 3x +1

Ist es überhaupt möglich so einfach die Nullstellen zu bestimmen?

Vielen Dank und noch einen schönen Sonntag!

Comments

Super, vielen Dank. Damit kann ich arbeiten =)

Answer 1

Bei ganzrationalen Funktionen dritten und vierten Grades ist es nicht so einfach. Dafür gibt's die Cardanische_Formeln. Bei fünften und höheren Grad muss man sogar oft auf numerische Verfahren zurückgreifen.

Answer 2

~plot~ x^3-3x+1~plot~

Wie du siehst gibt es keine ganzzahligen Lösungen.
Eine Berechnungsmöglichkeit wäre z.B. das Newtonverfahren.

Answer 3

Bekanntlich gilt \(\cos3z=4\cos^3z-3\cos z\) für alle \(z\in\mathbb R\).
Insbesondere gilt für \(z=\frac\pi9\)$$\frac12=4\cos^3\frac\pi9-3\cos\frac\pi9.$$Daraus folgt$$\left(-2\cos\frac\pi9\right)^3-3\cdot\left(-2\cos\frac\pi9\right)+1=0.$$

Answer 4

Neben den numerischen Lösungen wie Newton-Verfahren

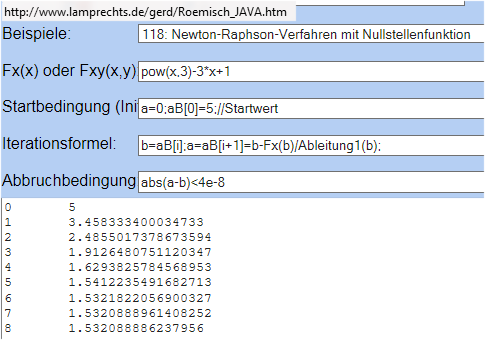
und/oder Bisektion

gibt es natürlich die Spezialfall-Behandlungen der

Cardanischen Formeln und Spezialfall-Betrachtung wie vom Gast beschrieben.

Es gibt aber auch bereits exakte fertige explizite PQRST-Formeln (kein Schulstoff, da komplexe Zwischenergebnisse!):

http://www.lamprechts.de/gerd/php/gleichung-6-grades.php

(LINK zur PQRST-Formel dort)

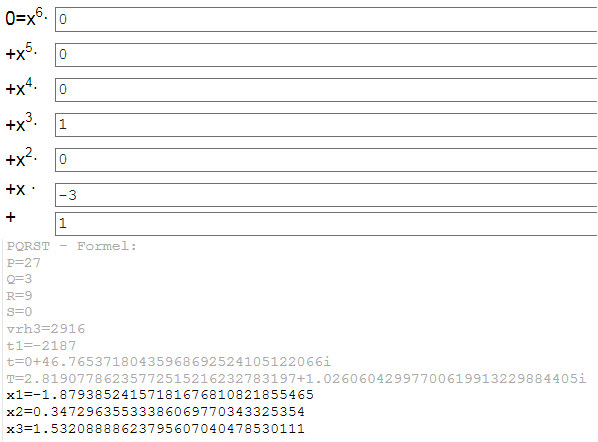
Hier ein gekürztes Ergebnis in exakter Schreibweise:

x3=1/(1/2 (-1 + i sqrt(3)))^{1/3} + (1/2 (-1 + i sqrt(3)))^{1/3} mit sqrt(3)=Wurzel(3)

Kein Lehrer wird Dir für diese exakte Formel einen Punkt geben, da er sie vermutlich selbst nicht kennt.