Tangente und Normale bestimmen. a) a) f(x) = 1 / x^2 , an B(1∣?) , f(0) = 0 = b?

Question

Tangenten und Normalen
Bestimmen Sie die Gleichung der Tangenten t(x) und die Gleichung der Normalen n(x) am Schaubild von f im
Punkt B:
a) f(x) = 1 / x^2      an B(1∣?)    f(0) = 0 = b????

f ' (x) = -2  /x ^3

f ' (1) = -2

y= mx + b    y= -2x + b

Wie geht es weiter?

Answer 1

f(x) = x^{-2}

f'(x) = - 2·x^{-3}

Tangente und Normale an der Stelle a

a = 1

f(a) = f(1) = 1

f'(a) = f'(1) = -2

t(x) = f'(a) * (x - a) + f(a) = -2 * (x - 1) + 1 = 3 - 2x

n(x) = -1/f'(a) * (x - a) + f(a) = -1/(-2) * (x - 1) + 1 = 1/2·x + 1/2

Answer 2

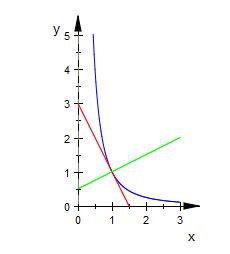
Der Punkt B hat die Koordinaten B (  1 | 1 ) und die Steigung ist -2.

Für die Tangente gilt dies auch. Tangentengleichung.

t ( x ) = m * x + b
t ( 1 ) = -2 * 1 + b = 1
-2 * 1 + b = 1
b = 3

t ( x ) = -2 * x + 3

Normale dazu
m ( Normale ) = -1 / ( -2 ) = 1 / 2
n ( x ) = 1 / 2  * 1 + b = 1
1 / 2  * 1 + b = 1
b = 1 / 2

n ( x )  = 1/2 * x + 1/ 2