Flächeninhalt mit bestimmtem Integral berechnen. Parabel, Tangente.

Question

:)

Also ich tu grad lernen für eine bevorstehende klausur und kenn mich bei einem beispiel nicht aus..ich weiß wie man es integriert aber welche fläche ist eigentlich gesucht ich kann mir das irgendwie nicht bildlich vorstellen :(

Beispiel: 

Berechne den inhalt der fläche die von der parabel f mit y=((-x^2)/4)+4, der tangente an f in P(2/y) und der x-achse umschlossen wird.

Bitte helft mir hersuszufinden welche fläche überhaupt gesucht wird und wie man das händisch ausrechnet, denn ich möchte es lernen und später selber schaffen

Lg & danke :)

Answer 1

f ( x ) = ( (-x²) / 4) +4 ;
Tangente
t ( x ) = m * x + b

Für eine Tangente ( Berührpunkt ) gilt
f ( x ) = t ( x )
f ´( x ) = t ´( x )

f ´( x ) = - 1/ 4 * 2 * x
f ´( x ) = - 1/2 * x
an der Stelle x = 2 ist die Steigung
f ´( 2 ) = - 1/2 * 2 =  - 1

Die Steigung hat auch die Tangente im Punkt x = 2 

t ( x ) = -1 * x + b
f ( 2 ) = +3
t ( 2 ) ist auch  3
3 = -1 * 2 + b
b = 5

t ( x ) = - x + 5

Hier der Graph

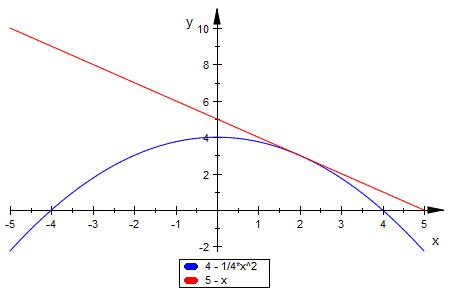
Bei Fragen wieder melden oder wenn es weitergehen soll.

Comments

Soweit bin ich auch gekommen :) mein problem ist nun, dass ich nicht weiß von welcher fläche hier auf dem graphen ich die fläche ausrechnen soll? Denn in der angabe steht ich sol die fläche ausrechnen die von der parabel, der tangente und x-achse umschlossen wird, nur kann ich die gefragte fläche nicht erkennen? 

---

Vom Berührpunkt nach rechts.
Die Fläche zwischen der blauen und der roten Kurve.
Nach unten zwischen x = 4 und x = 5 auf der x-Achse.

Falls die Beschreibung nicht ausreicht kann ich die
Grafik einstellen.

1.) Integral t ( x ) zwischen x = 2 und x = 5
2.) Integral f ( x ) zwischen x = 2 und x = 4

2 von 1 abziehen.

---

Super danke hat echt geholfen :)

Könntest du mir vl erklären warum man da bei x=2 anfängt? Macht man das, weil das der schnittpunkt ist oder wie geht das? 

---

Richtig.
Laut Aufgabenstellung soll die Tangente die Funktion an der Stelle x = 2 berühren
Also ist der Integrationsanfang für beide Flächen derselbe.

Das Integraionsende ist dann erreicht wenn die Funktionen die x-Achse schneiden.
Die Fläche endet dort.