Ich bin jetzt schon seit geraumer Zeit an dieser Aufgabe am
herumknobeln. Die Differenzfunktion, die wir noch nicht kennen, sieht
doch ungefähr so aus.
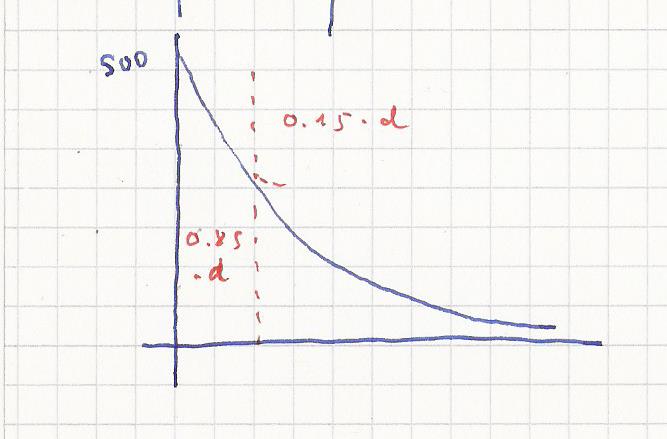
Die Differenz soll um 0.15 * d abnehmen ( oberer Teil )
Dann ist die neue Differenz 0.85 * d ( unterer Teil ).
Im nächsten Schritt passiert wieder dasselbe.
( d * 0.85 ) * 0.85 bleibt als neue Differenz übrig.
d ( x ) = 900 * 0.85^t
Der Bestand ist dann
b ( x ) = 1000 - d ( x ) = 1000 - 900 * 0.85^t
Dies entspricht der Formel des Mathecoachs bei deiner anderen Anfrage.
Man kann die Formel auch als e-Funktion schreiben.
b ( x ) = 1000 - d ( x ) = 1000 - 900 * e^{ln[0.85]*t}