Skalierung des Koordinatensystems

Question

Hi :)

Ich habe hier eine Aufgabe bei der ich einfach nicht weiter komme:
Gegeben ist der Graph einer ganzrationalen Funktion vom Grad n.

Vervollständigen Sie die Skalierung des Koordinatensystems so, dass die Fläche, die der Graph von f mit der x-Achse einschließt, den Flächeninhalt A hat.  (n= 3 , A= 216)

 

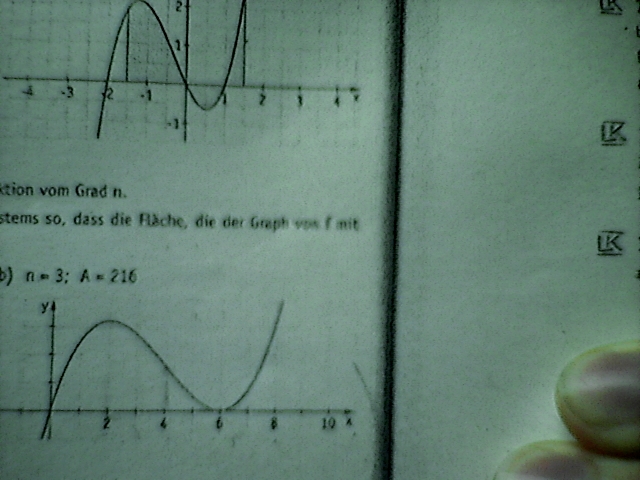
Ich habe versucht den Funktionsterm zu rekonstruieren, aber anscheinend kann ich die Bedingungen nicht einfach ablesen, denn egal welche ich genommen habe, konnte ich nicht nach einer Variabel auflösen....

Gibt es hier vielleicht einen bestimmten Trick, den ich nicht kenne?

Wäre toll, wenn mir Jemand helfen könnte :)

Ich hoffe man kann einigermaßen das Bild erkennen. ( Es ist der untere Graph ;) )

LG Luna

Answer 1

Es gibt eine Nullstelle bei x=0 und eine doppelte bei x=6.

Also f(x) = a * x *(x-6)^2

Das Integral von 0 bis 6 ist dann 108a

und damit das 216 ergibt muss a=2 sein.

Dann ist also f(x) = 2 * x *(x-6)^2

und f(2) = 64

Alöso ist der 3. Strich auf der y-Achse etwa bei 60

also die Einheit 20.

Answer 2

Vervollständigen Sie die Skalierung des Koordinatensystems so,
dass die Fläche, die der Graph von f mit der x-Achse einschließt,
den Flächeninhalt A hat.  (n= 3 , A= 216)

Ablesbar ist
f ( 0 ) = 0
f ( 6 ) = 0
f ´( 2 ) = 0
f ´( 6 ) = 0
sowie die Angabe

f ( x ) = a * x^3 + b * x^2 + c * x + d

Geht gleich weiter.

Comments

mathef hat die Antwort schon gegeben.
Falls noch Fragen sind dann wieder melden.

---

Die Bedingungen die du hattest hatte ich auch so.

0=d

0= 216 a + 36 b + 6 c +d

0=12a +4b + c

0= 108 a +12 b+ c

Nur ist mir nicht klar wie ich ab hier weiter machen soll. Es lässt sich einfach nicht richtig wegkürzen. Oder übersehen ich da was??

mathef´s Weg kann ich leider nicht nachvollziehen....

---

f(0) = 0 -> d= 0 ->  f(x) = ax³ +bx² + cx

f(6) = 0 ->  216a + 36b + 6c = 0 [G1]

f '(2) = 0 ->  12a + 4b + c = 0      [G2]

f '(6) =0 ->   108a + 12b + c =0   [G3]

Das LGS hat keine eindeutige Lösung:

Man erhält lediglich a = 1/36 c und b = -1/3 c,

Zu Mathefs Lösung:

f(x) = ax³ +bx² + cx + d  mit drei Nullstellen x₁ , x₂ und x₃ lässt sich immer umschreiben als

f(x) = a • (x-x₁) • (x-x₂) • (x - x₃)

Nullstellen bei Extremwerten sind dabei doppelte Nullstellen

---

Hat diese Umschreibung einen bestimmten Namen? 

---

Mit eurem Weg geht es auch, wenn auch aufwändiger:

0=d

0= 216 a + 36 b + 6 c +d

0=12a +4b + c

0= 108 a +12 b+ c

gibt

0= 216 a + 36 b + 6 c

0=12a +4b + c      --> c= -12a -4b

0= 108 a +12 b+ c

gibt

0=144a + 12b

0=96a + 8b   ---> b= -12a

also in der ersten

0=0.  d.h. Du kannst a wählen wie du willst( ungleich 0) und hast dann

b= -12a  und (s.o. ) c= -12a -4b= 36a  und dwar ja 0.

Also f(x) = ax^3 -12ax^2 +36ax

              = a ( x^3 -12x^2 +36x) [ Das ist mein a * x *(x-6)² ]

Jetzt das Integral von 0 bis 6 ausrechnen:

gibt  [1/4ax^4 - 4ax^3 + 18ax^2 ] in den Grenzen von 0 bis 6

= 108a

Es soll aber eine Fläche von 216 sein. Also a=2.

Dann ist f(x) = 2* ( x^3 -12x^2 +36x)

und wieder f(2)=64 etc.

---

Hat diese Umschreibung einen bestimmten Namen?
Ja. Zerlegung in Linearfaktoren.
Und wenn eine Nullstelle zugleich eine
Extremstelle ist, kommt der Linearfaktor (mindestens) doppelt
vor und bei Wendestellen mindestens dreifach.

---

ich habe das grad nur schnell überflogen und schau es mir gleich mal in Ruhe an, aber auf den ersten Blick scheine ich es zu verstehen.

vielen Dank!  :)

---

Na ist aj prima!

---

Aufgrund der Nullstelle bei x = 0 und der doppelten Nullstelle
bei x = 6  wäre eine mögliche Funktion
f (x )  = x * ( x - 6 )²

Alle jetzt aufgeführten Funktion haben dieselben Nullstellen
f (x )  = 1 * x * ( x - 6 )^2
f (x )  = 2 * x * ( x - 6 )^2
f (x )  = 3 * x * ( x - 6 )^2

oder allgemein
f ( x )  = a * x * ( x - 6 )^2

Jetzt wird nur noch die Funktion oder das a gesucht welches die
Fläche 216 ergibt.

Noch ein Bildchen für die Graphen mit verschiedenen a

~plot~ 1 * x * ( x - 6 )^2 ; 2 * x * ( x - 6 )^2 ; 3 * x * ( x - 6 )^2 ; [[ 0 |10 | 0 | 100 ]] ~plot~