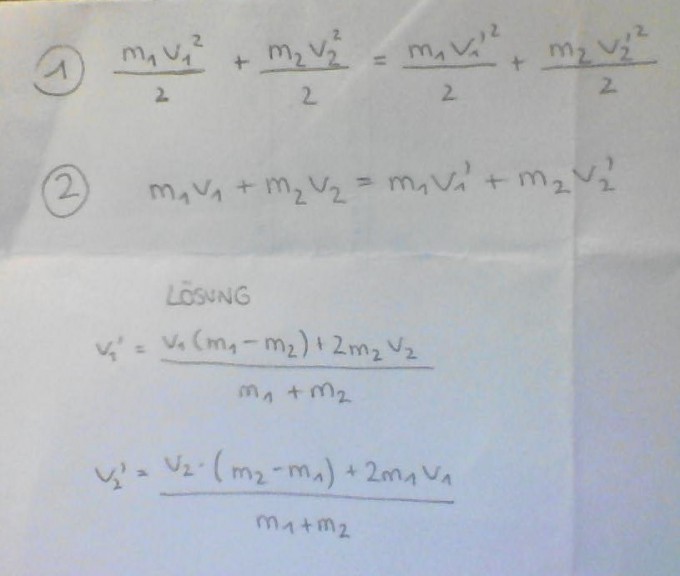Wie kann man aus diesem Gleichungssystem die beiden Unbekannten v1 und v2 bestimmen?

Question

Gleichung I: $$ \frac { m _ { 1 } v _ { 1 } ^ { 2 } } { 2 } + \frac { m _ { 2 } v _ { 2 } ^ { 2 } } { 2 } = \frac { m _ { 1 } v _ { 1 } ^2 } { 2 } + \frac { m _ { 2 } v _ { 2 } ^2 } { 2 } $$

Gleichung II: $$ m _ { 1 } v _ { 1 } + m _ { 2 } v _ { 2 } = m _ { 1 } v _ { 1 } ^ { \prime } + m _ { 2 } v _ { 2 } ^ { 1 } $$

Lösung:

$$ v _ { 1 } ^ { \prime } = \frac { v _ { 1 } \left( m _ { 1 } - m _ { 2 } \right) + 2 m _ { 2 } v _ { 2 } } { m _ { 1 } + m _ { 2 } } $$

$$ v _ { 2 } ^ { \prime } = \frac { v _ { 2 } \cdot \left( m _ { 2 } - m _ { 1 } \right) + 2 m _ { 1 } v _ { 1 } } { m _ { 1 } + m _ { 2 } } $$

Ich müsste aus diesem Gleichungssystem die beiden Unbekannten v1' und v2' bestimmen.

Ich habe jedoch keine Ahnung, wie ich das anstellen soll! Könnt ihr mir bitte helfen? Ich habe sehr viel ausprobiert, komme aber nicht auf die Lösung, die angegeben ist und ich bin echt am Verzweifeln.

Es wäre echt hilfreich, wenn ihr mir helfen könntet.

Comments

In der 1.Gleichung kann durch 2 entfallen.

Die 2.Gleichung nach v2´ umstellen.
v2´ in die erste Gleichung einsetzen und nach v1´
umstellen.
Die angegebene Lösung stimmt.
Allerdings scheint es viel zum umformen zu geben.

---

Das heißt, man kann die 2 bei der ersten Gleichung eigentlich wegstreichen?

---

@gast: richtig. Du rechnest die Gleichung "mal 2" dann sind die Nenner alle weg.

Answer 1

Vielleicht mag da mal wer drüberschauen - ich bin durch für heut...

I:$$ \frac{m \cdot v^2}2 + \frac{n \cdot w^2}2 = \frac{m \cdot x^2}2 + \frac{n \cdot y^2}2  $$ $$ m \cdot v^2 + n \cdot w^2 = m \cdot x^2 + n \cdot y^2  $$
II:$$ m \cdot v + n \cdot w = m \cdot x + n \cdot y  $$
$$ m \cdot v + n \cdot w - m \cdot x = n \cdot y  $$
$$ m \cdot (v-x) + n \cdot w  = n \cdot y  $$
$$ \frac m n \cdot (v-x) +  w  =  y  $$
Einsetzen in I:
 $$ m \cdot v^2 + n \cdot w^2 = m \cdot x^2 + n \cdot \left( \frac m n \cdot (v-x) +  w  \right)^2  $$
 $$ m \cdot v^2 + n \cdot w^2 = m \cdot x^2 + n \cdot \left( \frac m n \cdot (v-x)\right)^2   +2\left( \frac m n \cdot (v-x) \cdot  w  \right)+  w  ^2$$
 $$ m \cdot v^2 + n \cdot w^2 = m \cdot x^2 +  \frac {m^2} n \cdot \left( v-x\right)^2   +\frac {2 \cdot m\cdot  w} n \cdot \left(  v-x   \right)+  w  ^2$$
 $$ m \cdot v^2 + n \cdot w^2 = m \cdot x^2 +  \frac {m^2} n \cdot \left( v^2-2vx+x^2\right)   +\frac {2 \cdot m\cdot  w} n \cdot \left(  v \right)-\frac {2 \cdot m\cdot  w} n \cdot \left( x \right)+  w  ^2$$
 $$ m \cdot v^2 + n \cdot w^2 = m \cdot x^2 +\frac {m^2} n \cdot \left(x^2\right) + \frac {m^2} n \cdot \left( -2vx\right) + \frac {m^2} n \cdot \left( v^2\right)   +\frac {2 \cdot m\cdot  w \cdot   v } n -\frac {2 \cdot m\cdot  w} n \cdot \left( x \right)+  w  ^2$$
 $$ m \cdot v^2 + n \cdot w^2 =\left( m  +\frac {m^2} n \right)\cdot x^2 - \frac {2vm^2} n \cdot \left( x\right) + \frac {m^2 \cdot  v^2} n   +\frac {2 \cdot m\cdot  w \cdot   v } n -\frac {2 \cdot m\cdot  w} n \cdot \left( x \right)+  w  ^2$$
 $$ m \cdot v^2 + n \cdot w^2 =\frac { m n +m^2} n \cdot x^2 - \frac {2vm^2} n \cdot \left( x\right) -\frac {2 \cdot m\cdot  w} n \cdot \left( x \right)+ \frac {m^2 \cdot  v^2} n   +\frac {2 \cdot m\cdot  w \cdot   v } n +  \frac{w^2 n}n $$
$$ m \cdot n \cdot  v^2 + n^2 \cdot w^2 =( m n +m^2)  \cdot x^2 - 2vm^2 \cdot \left( x\right) -2 \cdot m\cdot  w \cdot \left( x \right)+ m^2 \cdot  v^2   +2 \cdot m\cdot  w \cdot   v  +  w^2 $$

Comments

Zuerst, vielen vielen Dank für deine Unterstützung und deine Hilfe!!! Also in der Art habe ich verstanden, wie Sie angefangen haben und bin Ihnen sehr dankbar, doch die Rechnung ist noch nicht ganz fertig, oder? Wie geht denn das weiter? Nach was soll ich das denn umstellen?Julia

---

Wie würde denn diese Gleichung weitergehen und was meinen Sie mit dem Fehler in der Umstellung? Welchen Fehler? Ich muss diese Gleichung bis spätestens heute Abend gelöst haben!

Danke und liebe Grüße Julia