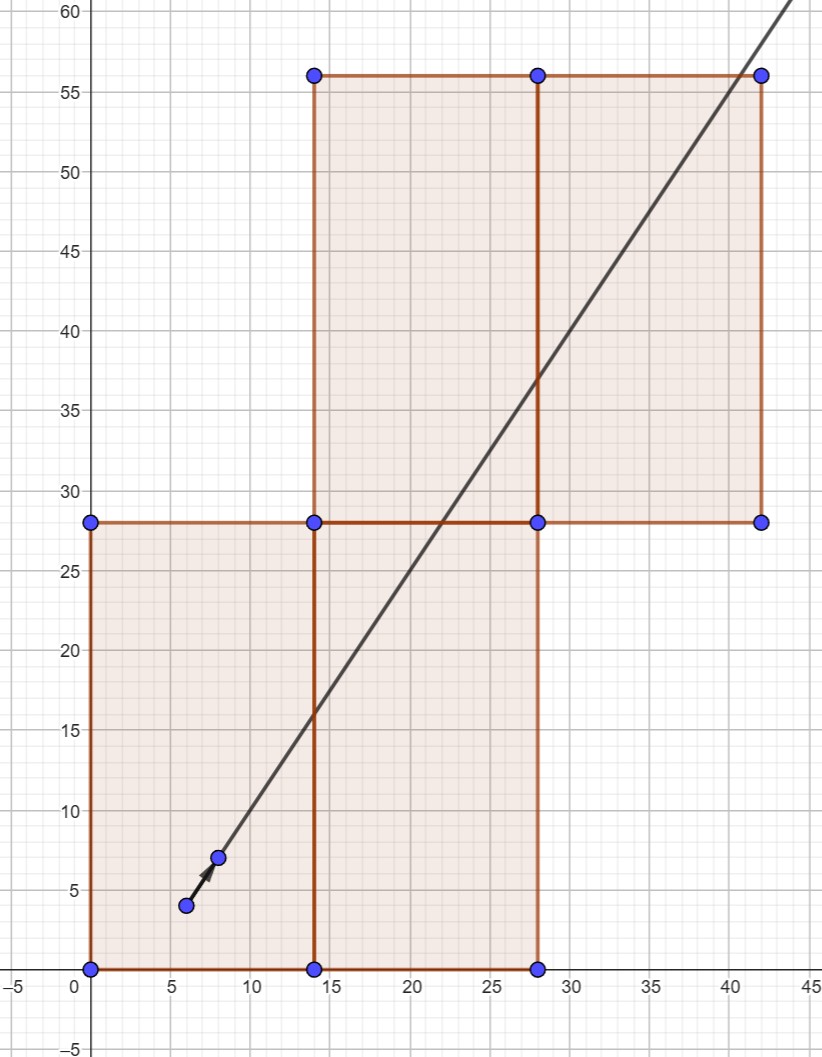
Anderer Weg. Statt sich die Bahn der Kugel an der Bande gespiegelt vorzustellen, denken wir uns den Tisch an der Bande gespiegelt vor. Dann bleibt die Bahn der Kugel einfach eine Gerade.
Man sieht bereits, dass die Ecke nicht getroffen wird.
[6, 4] + r·[2, 3] = [42, 56] → Keine Lösung
[6, 4] + 4·[9, 13] = [42, 56] → Das wäre eine Lösung.
Die Kugel müsste also z.B. in Richtung des Vektors [9, 13] geschossen werden.
Weiterhin kann man zeigen, dass
[6, 4] + r·[2, 3] = [14·m, 28·n] keine Lösungen für ganzzahlige Werte von m und n besitzt.