Wie hoch über dem Boden befindet sich der Mittelpunkt der Schaukel?

Question

Kann mir jemand bitte erklären, wie ich das rechne? 

"Wie hoch über dem Boden befindet sich der Mittelpunkt der Schaukel, wenn die Schaukel

a) um 30°  b) um40° c um 60°    ausgelenkt ist?"

Comments

Also ich kann dir nur die Länge der Aufhängung der Schaukel sagen (Hatte noch keine Trigonometrie). Das Seil ist:

√(2.5²-1.2²)m - 0.49m ≈ 1.70317122m

lang...

Vielleicht hilft das ;-)

 

Grüsse

Simon

Answer 1

Die Länge hat Simonai schon richtig berechnet   l= 1,703m Abstand vom Boden 0,49m

Mein Vorschlag wäre es mit proportionaler Zuordnung die Aufgabe zu lösen.

Bei einem Auschlag von 90° wäre die Schaukel  1,073+0,49  =2,193m  vom Boden entfernt

           90°                         1,703  +0,49

            :9                               :9

            10°                         0,189+0,49       

a)     3*10°=30 °                 0,4676m+0,49 m=0,9576m

b)      4*10°=40  °               0,75688+0,49m=1,24688m

c)      6*10°=60 °                1,1353m+0,49m=1,6253m

Comments

Ich habe jetzt eine 2. Frage hier gestellt, auch so eine ähnliche Aufgabe. Kann man das auch mit dieser Methode lösen?

https://www.mathelounge.de/28736/pfosten-hoch-lang-sind-schatten-abendsonne-horizont-steht

---

Ist nur ein Vorschlag, ansonsten müsste man es sehr umständlich  mit Winkelinnensummensatz und tan und/oder  sin  berechnen. Aufgabe habe ich schon gesehen.

---

Die oben gemachten Angaben sind falsch! Hier kommt man nur über den Kosinussatz zu den richtigen Ergebnissen.

a) ~72 cm

b) 89 cm

c) 134 cm

Answer 2

Berechnungsbild: Auslenkung \(α=30°\)

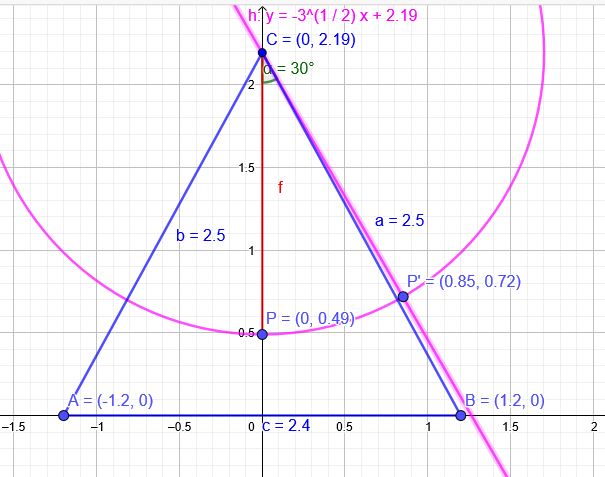
Berechnung der Höhe des Schaukelgestells:

\(h^2+1,2^2=2,5^2\)      \(h^2=2,5^2-1,2^2=4,81\)       \(h=2,193\)

Geradengleichung durch C\((0|2,193)\)  mit \( m=-\tan(60°)= -\sqrt{3} \)

\(y=-\sqrt{3}x+2,193\)

Kreis um C\((0|2,193)\) mit \(r=2,193-0,49=1,703\)

\(x^2+(y-2,193)^2=2,9\)

Schnitt mit \(y=-\sqrt{3}x+2,193\)

\(x^2+(-\sqrt{3}x+2,193-2,193)^2=2,9\)

\(4x^2=2,9\)

\(x^2=\frac{2,9}{4}\)

\(x=0,85\) Geschnitten mit \(y=-\sqrt{3}x+2,193\)

\(y=-\sqrt{3}\cdot 0,85+2,193=0,72\)m