Hilfe bei folgenden Aufgaben der Analyis

Question

bräuchte mal bitte ein paar Ansätze/Lösungen zum bearbeiten folgender Aufgaben, sind aus einem Übungstextbuch, komm aber grad nich dahinter.

Bedanke mich für jede Hilfe.

Comments

Hi,
bei Aufgabe 3 hast Du ja zwei Nullstellen gegeben. Eine dritte kann man sofort ablesen, nämlich \( z = 0 \) Da auch eine komplexe Nullstelle vorgegeben ist, weiss man das auch das konjugierte eine Nullstelle ist. Damit hat man vier Nullstellen. Nach Polynomdivision bleibt dann nur noch eine quadratische Gleichung übrig, de man normal lösen kann.

Answer 1

Hallo

Aufgae 3

Klammere zuerst z aus .Dann faktorisiere oder führe eine  Polynomdivision durch

Lösung: z(z-1)(z+2)(z+3)(z^2+1)=0

Answer 2

 

A2:

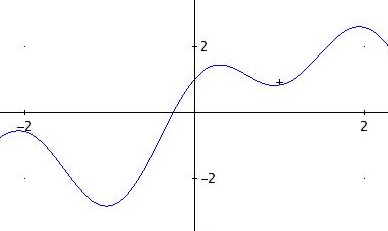
f ist stetig,  jede stetige Funktion nimmt auf einem abgeschlossenen Intervall ein Minimum und ein Maximum an.

f(-1) ≈ -2,828427124 <0  und f(1) = 2·√2 - 2 >0

Zwischenwertsatz → f hat im Intervall [-1;1] mindestens eine Nullstelle.

A3:

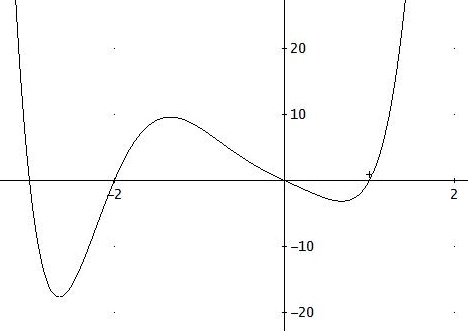
x ausklammen, Nullstelle x=1 der Klammer durch Probieren,

Polynomdivision:   (x⁵ + 4·x⁴+ 2·x³ - 2·x² + x - 6) : (x-1) =  x⁴ + 5·x³ + 7·x² + 5·x + 6

Nullstelle x= -2 durch Probieren:

(x⁴ + 5·x³ + 7·x² + 5·x + 6) : (x+2) = x³ + 3x² + x + 3

Nullstelle x= -3 durch Probieren:

Polynomdivision:  ( x³ + 3x² + x + 3) : ( x+3) = x² +1

keine weiteren Nullstellen.

Gruß Wolfgang