L'Hospital: Zeige, dass für alle n element N gilt..

Question

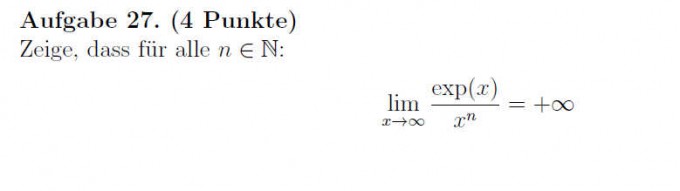
Ich bin mir total unsicher wie die Aufgabe gelöst werden muss..

Ich hatte die Idee das nach dem n-ten Mal ableiten ja im Nenner eine Konstante steht und im Zähler weiterhin e^x. Dann würde der Zähler gegen ∞ gehen und der nenner gegen n!     (?  oder (n+1)!   ?)  und somit ist der limes ja ∞/n! (oder n+1!)

Wie kann ich das Problem lösen? Ich hatte noch an Induktion gedacht (einfach nur weil es für jedes n bewiesen werden soll) bin mir aber auch da ziemlich unsicher.

LG Denise

Answer 1

Vielleicht auch mithilfe der Exponentialreihe. Sei \(n\in\mathbb N\). Für alle \(x>0\) gilt$$\exp(x)=\sum_{k=0}^\infty\frac{x^k}{k!}>\frac{x^{n+1}}{(n+1)!}.$$Daraus folgt$$\frac{\exp(x)}{x^n}>\frac x{(n+1)!}\xrightarrow{\ x\to\infty\ }\infty.$$

Comments

hm das thema unseres blattes ist l'hospital.

hast du dazu irgendeine idee?

---

Wie bereits vermutet ist dann wohl Induktion gefragt.
$$(1)\quad\lim_{x\to\infty}\frac{\exp(x)}x=\lim_{x\to\infty}\frac{\exp(x)}1= \infty.$$$$(2)\quad\lim_{x\to\infty}\frac{\exp(x)}{x^{n+1}}=\lim_{x\to\infty}\frac{\exp(x)}{(n+1)x^n}=\frac1{n+1}\lim_{x\to\infty}\frac{\exp(x)}{x^n}\overset{\color{blue}{\small\text{IV}}}=\infty.$$

---

Funktioniert denn der Induktionsanfang auch für x=1?

---

Induktion erfolgt hier über \(n\), nicht über \(x\).

---

ja das meinte ich natürlich. entschuldige den fehler :)

---

Was oben unter (1) steht, ist der Induktionsanfang.

---

schon wieder entschuldige den fehler. es war ja für n=1. x¹ ist ja x und das abgeleitet ist ja 1...

Ist schon etwas spät... :D

aber danke für deine hilfe! dann lag ich ja mit meiner idee doch gar nicht so falsch :)

---

Dem kann ich zustimmen.

---

https://www.mathelounge.de/291379/grenzwertberechnung-lhospital#c291392

Falls du noch Lust hast mir bei einer weiteren L'Hospital Aufgabe zu helfen ;)

---

Also ist das soweit vollständig oder kann man noch irgendwas hinzufügen?

---

Man könnte vielleicht noch erwähnen, dass l'Hospital hier anwendbar ist. Ansonsten sollte das völlig ausreichen.

---

Kann mir jemand kurz nochmal erklären was beim Induktionsschritt gemacht wurde?