zyklische Gruppe und die Untergruppen

Question

hallo

Sei (Z/nZ, [+] ) eine zyklische Gruppe.

Ich soll die Unterguppen für Z/5Z und Z/6Z bestimmen.

Also:

Für Z/5Z...

Untergruppe sind - Z/Z = {0} und Z/5Z ={0, 1, 2, 3, 4}

Für Z/6Z...

Untergruppen sind -  Z/Z = {0,  Z/2Z = {0, 3} ,  Z/3Z = {0, 2, 4} und Z/6Z ={0, 1, 2, 3, 4, 5}

Ist die Notation so richtig?

wie kann ich es schön (bzw. kurz) zeigen, dass diese wirklich Untergruppen sind und es keine weiteren gibt.

Man kann leicht nachprüfen, dass es sich wirklich um Untergruppen handeln. (neutrales Element 0, und die Inversen). Aber ich muss doch ausschließen können, dass es keine weiteren Untergruppen geben kann. Oder reicht es einfach diese Untergruppen aufzuschreiben?

Die Aufgabe lautet nämlich: Bestimmen Sie alle Untergruppen...

Ich habe diesen Satz gefunden:

...................................

Hat G ={e, g, g², g³, ... g^{n - 1}} die Ordnung n, so gibt es zu jeder natürlichen Zahl d, die n teilt, genau eine zyklische Untergruppe U_d der Ordnung d von G, die von 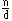erzeugt wird

.......................................

Ist dieser Satz relevant für meine Aufgabe? (falls nicht, bitte den Satz einfach ignorieren)

Dankee für jede Antwort.