Funktionssuche 3. Grades.

Question

könnt ihr mir hier weiterhelfen:

Bestimme die ganzrationale Funktion 3. Grades, deren Graphen die X Achse im Punkt P (4/0) berührt und im Ursprung die Tangente mit der Gleichung y=4x besitzt.

=> 3. Grad ist ja : ax^3 + bx^2 + cx + d

nun weiss ich nicht mehr

=> Wie kann ich weiter berechenn?

Answer 1

Bestimme die ganzrationale Funktion 3. Grades,

f(x) = ax^3 + bx^2 + cx + d

deren Graphen die X Achse im Punkt P (4/0) berührt

f(4) = 0

64·a + 16·b + 4·c + d = 0

f'(4) = 0

48·a + 8·b + c = 0

und im Ursprung

f(0) = 0

d = 0

die Tangente mit der Gleichung y=4x besitzt.

f'(0) = 4

c = 4

Nun haben wir 4 Gleichungen mit 4 Unbekannten. Das ist ein Gleichungssystem welches man mit dem Additionsverfahren lösen kann.

Eine Lösung ist hier: a = 1/4 ∧ b = -2 ∧ c = 4 ∧ d = 0

Die Funktion lautet daher

f(x) = 1/4*x^3 - 2*x^2 + 4*x

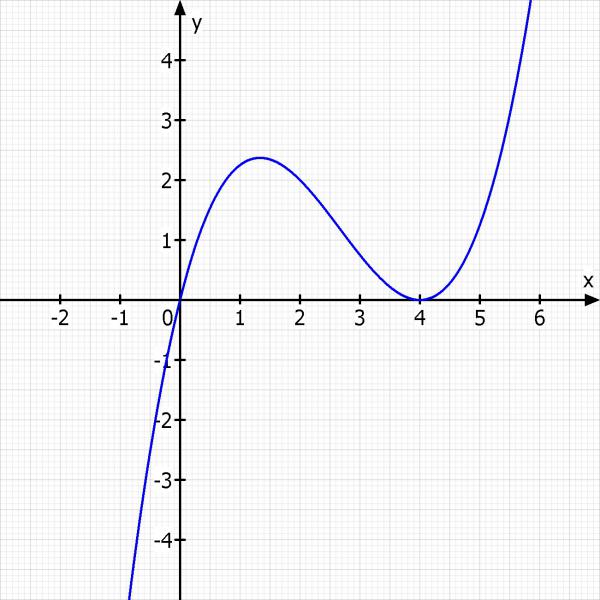
Skizze:

Answer 2

Du hast einmal den Punkt (4,0) die vom Graphen berührt wird, also

0=a*4^3+b*4^2+c*4+d

und da in der Aufgabenstelleung "berührt" steht muss der Punkt ein Minimum oder Maximum sein, also die Zweite Ableitung für x=4 Null sein:

f'=3*a*x^2+2*b*x+c

3*a*4^2+2*b*4+c=0

Außerdem geht der Graph noch durch den Ursprung:

also
0=a*0^3+b*0^2+c*0+d -> d=0

und die Tangentensteigung in dem Punkt ist 4 also muss

4=3*a*0^2+2*b*0+c ->c=4

jetzt bleibt noch übrig: (c und d eingesetzt)


64a+16b+16=0

24a+8b+4=0

=>aus der ersten Gleichung:  a=(-1-b)/4
=> 6(-1-b)+8b+4=0 => 2b=2 => b=1
=> a=-1/2
also ist die Funktion f(x)=-1/2 x^3+x^2+4x