Leibnizkriterium bei Summe von (-1)^n * ( 1+1/n)^n?

Question

Hallo , ich soll die unten genannten Reihe auf Konvergenz und absolute Konvergenz prüfen.

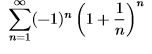
Da die Reihe eine alternierende Reihe ist , dachte ich mir Leibniz zu verwenden.Hierbei müssen Monotonie und eine Nullfolge erfüllt sein. Jedoch bildet  (1 +1/n)^n keine Nullfolge . dieser Ausdruck geht für n gegen unendlich , zu e .

Was heißt das nun das die Reihe divergiert? Oder das man hierbei mit Leibnitz keine Aussage treffen kann?

Bzw. wie würde man das ansonsten auflösen?

Bitte um eine Antwort , Danke !

Comments

ich habe bemerkt das Bild wurde nicht richtig hochgeladen !

---

EDIT: Habe das Bild oben eingefügt.

Answer 1

(1 + 1/n)^n  ---------> e

Eulersche Zahl.

Daher ist (1+1/n)^n keine Nullfolge und

(-1)^n (1 +1/n)^n auch nicht.

Folgerung: Die Reihe konvergiert nicht.

Hat aber nichts mit Leibnizkriterium zu tun.

https://de.wikipedia.org/wiki/Gottfried_Wilhelm_Leibniz

Comments

Ah ok , ich glaube du meinst wegen der Nullfolgeneigenschaft der Reihenglieder ist notwendig für jede konvergente Reihe. ?

Ich dachte immer wenn der Leibnitz nicht funktioniert dann ist die Reihe immer divergent .Dabei ist das nur ein KonvergenzKriterium.

---

Beides richtig.

1. Du musst ein anderes Kriterium verwenden.

2. Nicht - Leibniz ist nicht Beweis genug für Divergenz.

---

Ok alles klar. Und in diesem Fall hat man einfach die Eigenschaft  der Nulffolge benutzt um eine Aussage zu treffen. Ich dachte immer man muss die Kriterien die man überlicherweise für Konvergenztests benutzt , zb VGL WK Qk usw , nutzen.