Konvergenz von Reihen mit Leibnizkriterium an+1 <= an!

Question

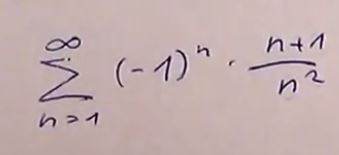
Darf ich hier eigentlich das Limes n gegen ∞ verwenden bei der Rechnung a_n+1<=a_n?

Ich meine so:

$$\lim _{ n\rightarrow \infty  }{ \frac { n+1+1 }{ (n+1)² } \cdot \frac { n+1 }{ n² }  } $$

<=> 0 ≤ n+1 ---> das kommt am Ende raus.

Oder muss ich das ohne machen wie hier?

Answer 1

Die 2. Version ist die richtige.

Der Grenzwert sagt ja nur was aus für sehr große Werte von n,

du brauchst aber eine Aussage über ALLE n.

Comments

sry ist lange her aber ich wiederhole alles wieder für die Klausur:

wegen:

"du brauchst aber eine Aussage über ALLE n"

gibts es da einen schnellen weg oder muss ich dafür eine vollständige Induktion machen?

Answer 2

ja es geht ohne Induktion, bringe auf den Hauptnenner:

a(n+1)-a(n)

=(n+2)/(n+1)^2 -(n+1)/n^2

=-(n^2+3n+1)/[n^2(n+1)^2]<=0