Wie kann ich das aber sehen wenn ich die Funktion nicht vor augen habe=?
Mit anderen Worten, woher sollte ich wissen ob dieses einzige Extremum
lokal oder absolut ist? Wie könnte ich das einfach feststellen?So einfach feststellen kann man das nicht. Es ist schon eine kleine
Kurvendiskussion vonnöten.
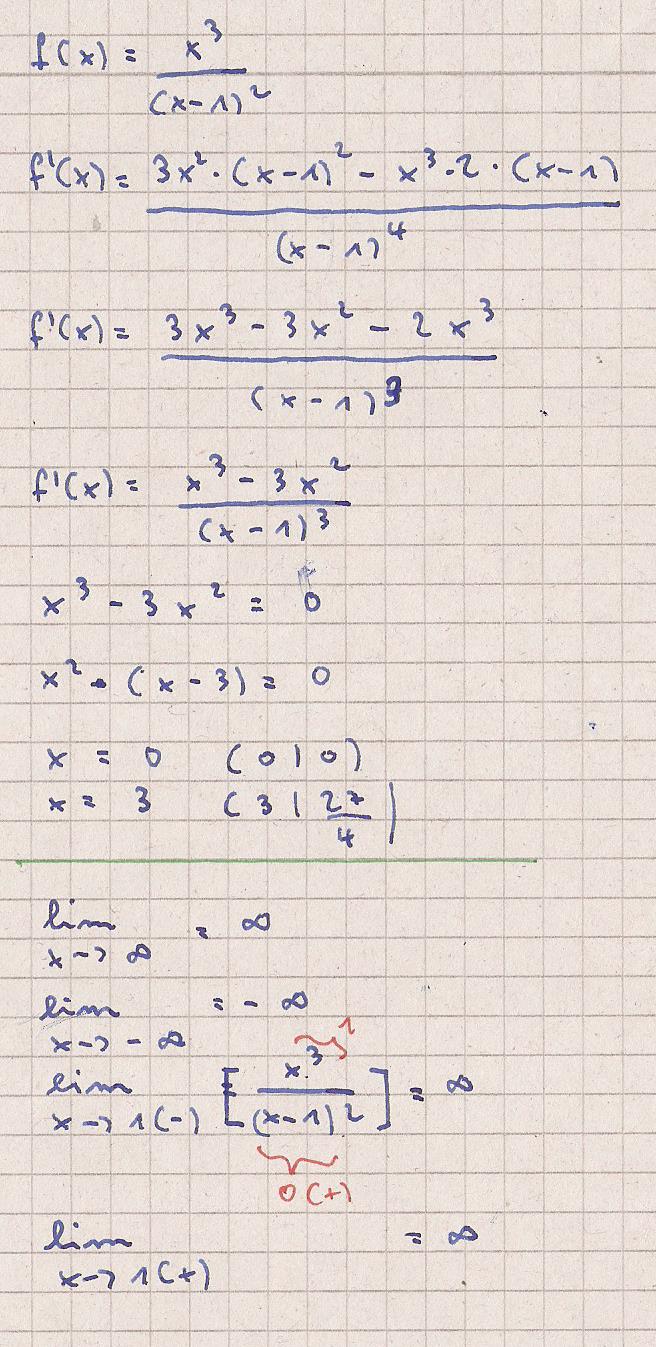
Die Funktion hat eine Polstelle und damit den Def-Bereich
D = ℝ \ { 1 }
Zunächst wurde die 1.Ableitung gebildet und die Stellen
mit waagerechter Tangente berechnet.
( 0 | 0 )
( 3 | 27 / 24 )
Jetzt müßte eine händische Berechnung der 2.Ableitung erfolgen. Dazu bin ich
zu faul. Mein Matheprogramm sagt :
( 0 | 0 ) Sattelpunkt
( 3 | 27 / 24 ) Tiefpunkt
Verhalten der Funktion an den Rändern des Def-Bereichs bestimmen.
-∞ , 1(--) , 1(+), ∞
Es ergibt sich.
lim x −> -∞ = - ∞
lim x −> 1(-) = + ∞
lim x −> 1(+) = + ∞
lim x −> ∞ = + ∞
Globales Minimum : minus unendlich
Globales Maximum : plus unendlich
lokales Minimum : ( 3 | 27 / 24 )