f(x) = 200000·x/(x + 1) - 2·x^3 - 101·x - 200
f'(x) = 0
200000/(x + 1)^2 - 6·x^2 - 101 = 0
- 6·x^4 - 12·x^3 - 107·x^2 - 202·x + 199899 = 0
6·x^4 + 12·x^3 + 107·x^2 + 202·x - 199899 = 0
Über eine Wertetabelle vermutet man zwei Nullstellen. Eine zwischen -14 und -13 und eine zwischen 12 und 13. Über ein Näherungsverfahren bekommt man dann:
x1 = -13.73582186 und x2 = 12.68976500
f(x1) = 222074
f(x2) = 179822
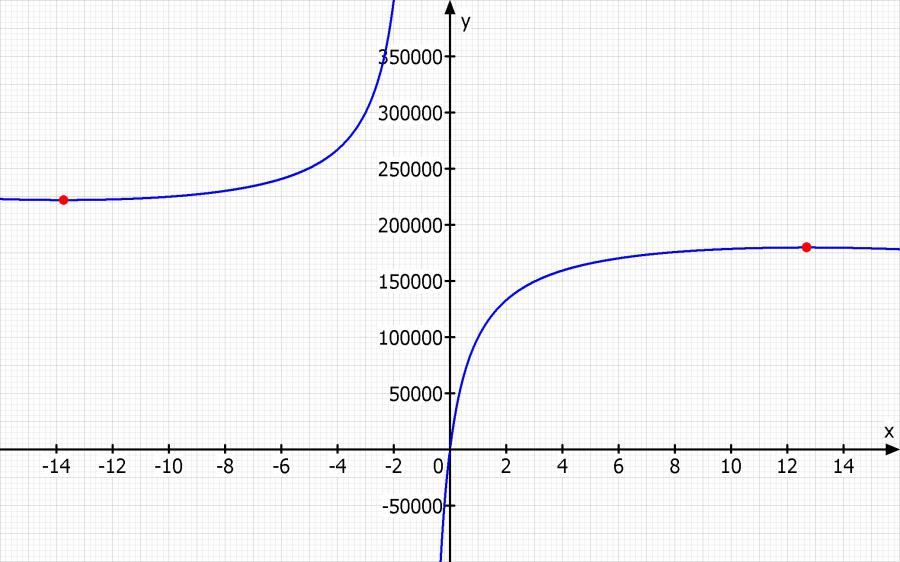
Skizze: