⇒Ziemlich viele Aufgaben für eine Frage.
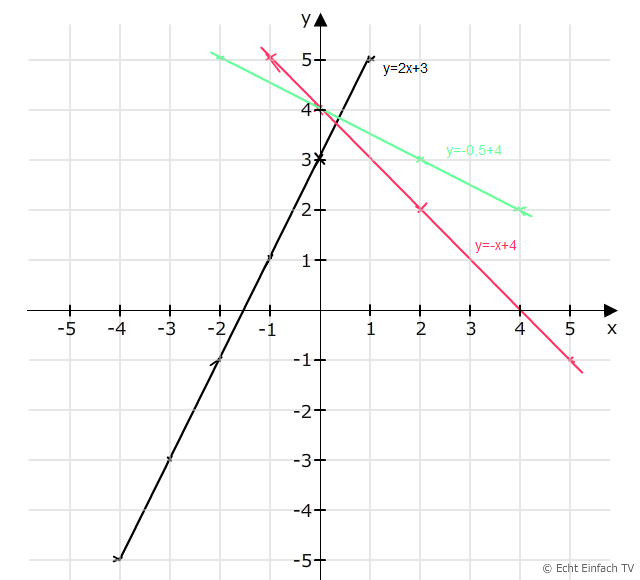
a) y=2x+3
Wertetabelle| x | -2 | -1,5 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | -1 | 0 | 1 | 3 | 5 | 7 | 9 | 11 |
diese Punktepaare in ein Koordinatensystem eintragen und verbinden.
b) aus der Funktion erkennt man bei x=0 ist y=3 (Schnittpunkt mit der y-Achse) von da aus legt man die Steigung an , die durch den Parameter 2 bei x angegeben wird nämlich 2:1 positiv, verlängern und schon hat man die Gerade.
c) Zeichnerisch einfach den Punkt eintragen und schauen ob er aucf der Geraden liegt. Rechnerisch für x=2 die Funktion berechnen y=2*2+3 ⇒ y=7 ( Siehe Wertetabelle) stimmt also.
d) zeichnerisch ablesen , rechnerisch muss y=0 sein also 0=2x+3⇒ -3/2=x Nullstelle bei (-1,5|0)
e) für einfach die Vorzeichen vertauschen y=-2x-3 Spiegelung an der x-Achse
f) nur für die Steigung das Vorzeichen wechseln y=-2x+3 Spiegelung an der y-Achse
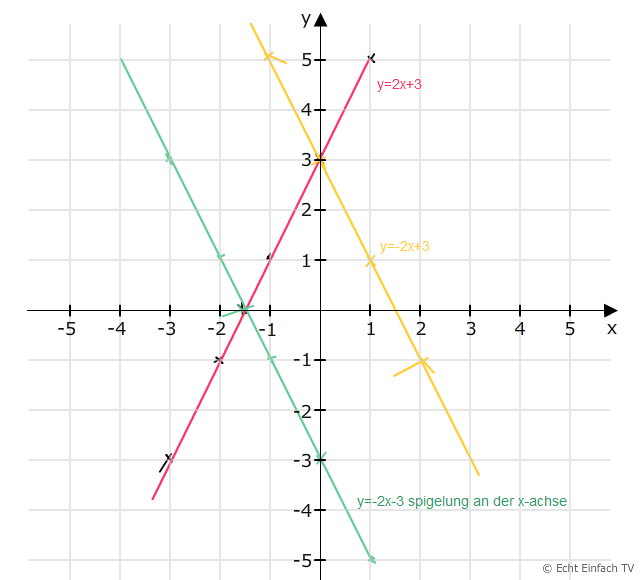
g) Punkt eintragen und verbinden.
h) Punkte in die allgemeine lineare Form einsetzen y=mx+b
5=m*(-1)+b
2=m*2+b Additionsverfahren anwenden und dann wieder einsetzen ⇒ y=-x+4
i) für den Schnittpunkt beide Geraden gleichsetzen
2x+3=-x+4 ⇒ x=1 dann erhält man S( (1/3) | 3 2/3)
j) Punkt einzeichnen, Lot daraufsetzen , entweder mit dem Zirkel oder mit dem Geodreieck.
k) Steigung ist -1/2
l) y=-0,5x+4