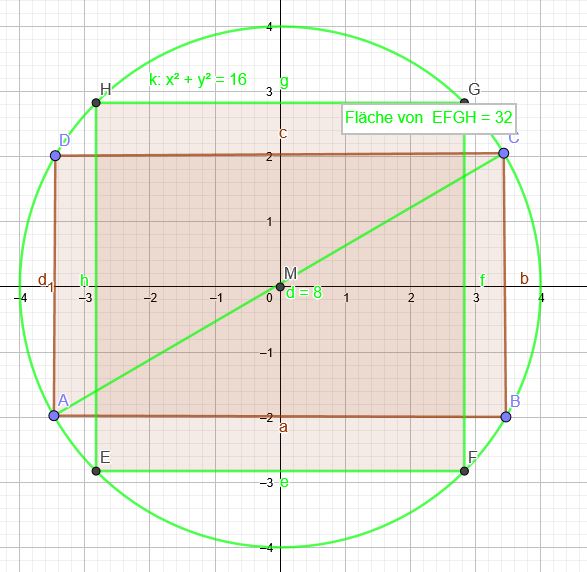
Zielfunktion:
\(A(a,b)=a*b\) soll maximal werden
Nebenbedingung:
\( a{^2} +b^2=64\)→\( b^2=64-a^2\) → \( b=\sqrt{64-a^2}\) -Wert entfällt.
\(A(a)=a*\sqrt{64-a^2}=\sqrt{64a^2-a^4}\)
\(A´(a)=\frac{128a-4a^3}{2\sqrt{64a^2-a^4}}=\frac{64a-2a^3}{\sqrt{64a^2-a^4}}\)
\(\frac{64a-2a^3}{\sqrt{64a^2-a^4}}=0\)
\(32a-a^3=0\)
\(a*(32-a^2)=0\)
\(a_1=0\) entfällt
\(a= \sqrt{32}=4*\sqrt{2} \)
\( b=\sqrt{64-32}=4*\sqrt{2}\)
\(A(4*\sqrt{2},4*\sqrt{2})=4*\sqrt{2}*4*\sqrt{2}=32FE\)