Korrekturen an deinem Handschriftlichem
Fall 1. ist soweit schon ganz gut bis auf das Ergebnis
x < 1.8
x < -1.3
und die dazu angefertigte Skizze.
Ich gehe bei der Lösung der Ungleichung
x^2 - x - 5
< 0 wie folgt vor.
Der linke Teil ist eine Parabel
Davon rechne ich die Nullstellen aus indem ich annehme
x^2 - x - 5
= 0 | pq-Formel
x = 1.8
x = -1.3
Einzeichnen der Werte auf einem Zahlenstrahl
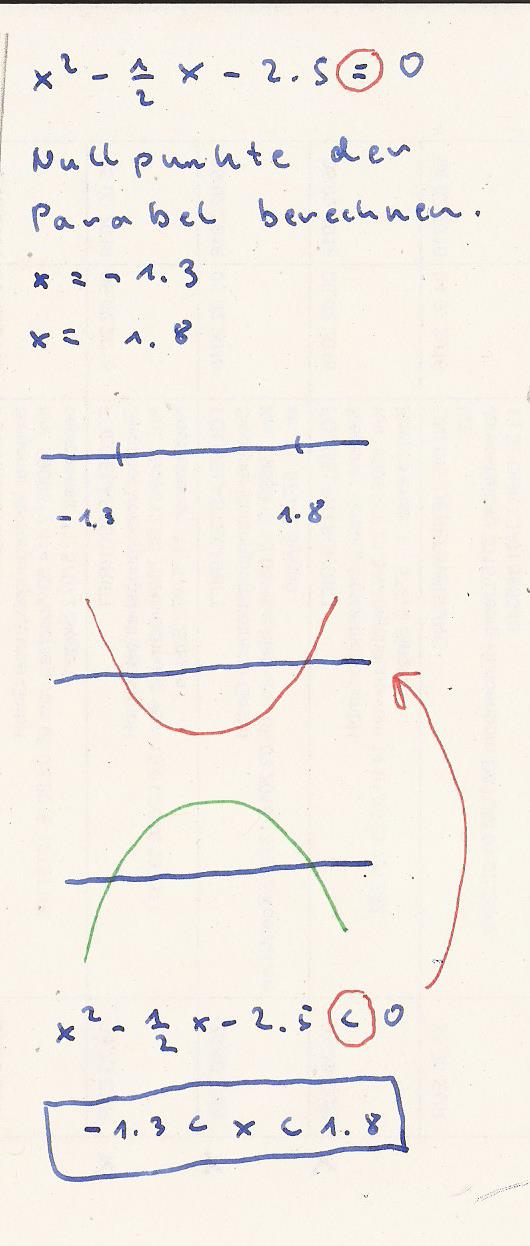
Die Parabel kann noch oben geöffnet sein ( rote Parabel )
oder
nach unten geöffnet sein ( grüne Parabel )
Da das Vorzeichen von
+2*x^2 - x - 5 < 0
positiv ist handelt es sich um
eine nach oben geöffnete Parabel ( rote Parabel )
Zwischen -1.8 < x < 1.3 wäre der Funktionswert kleiner 0
Dies ist die Lösung.
Eine weitere Methode wäre " die Punktprobe ".
x^2 - x - 5
= 0
x = 1.8
x = -1.3
Es wird ein Punkt zwischen x = -1.3 und x = 1.8 angenommen.
Ist der Funktionswert < 0 so ist der ganze Bereich zwischen
x = -1.3 und x = 1.8 kleiner 0.
f ( -1) = (-1)^2 - (-1) - 5 = -3
Der Funktionswert ist kleiner 0.
-1.8 < x < 1.3 ist die Lösung.