!
Vorneweg: Meine Schulzeit ist inzwischen über 20 Jahre her und beruflich habe ich ebenfalls nichts mit Mathematik zu tun. Ich habe nur einen Realschulabschluss und deswegen von vielen mathematischen Sachen noch nicht gehört. Trotzdem habe ich seit einiger Zeit ein großes Interesse, folgenden Vorgang in eine Gleichung zu fassen oder ihn anderweitig mathematisch zu beschreiben. Ich hoffe, ich habe alle Parameter bedacht, die zu einer Lösung führen könnten.
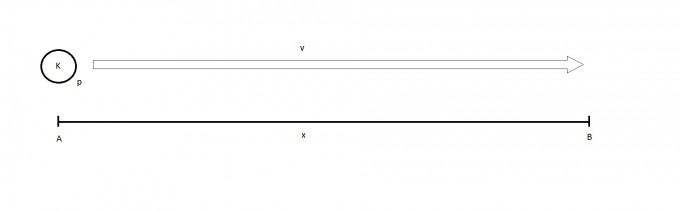
Gegeben sei eine Strecke 'x' zwischen einem Punkt A und einem Punkt B.
Ein Behältnis 'K' mit dem Druck 'p' im Inneren befindet sich an Punkt A.
Nun bewegt sich Behältnis 'K' mit konstanter Geschwindigkeit 'v' von Punkt A zu Punkt B und der Druck 'p' im Behältnis 'K' erhöht sich nach folgendem Prinzip:
Halbiert sich der Abstand 'x', so verdoppelt sich der Druck 'p'. Ausgeschrieben wäre das 1/2 x = 2 p (wie gesagt, meine Schulzeit ist lange her)
Sobald Behältnis 'K' Punkt B erreicht, fällt der Druck 'p' auf 0.
Nun ergibt sich folgendes Problem:
Der Abstand lässt sich nach diesem Prinzip immer nur halbieren, Punkt B würde aber nie erreicht werden, während der Druck sich immer weiter erhöhen würde. Gibt es denn einen Weg, diesen Vorgang mathematisch zu beschreiben?
Über Hilfe hierbei würde ich mich wirklich sehr freuen.
Vielen Dank schonmal im Voraus!
Waton