Unter der Voraussetzung das es sich um eine stetige Funktion handeln soll würde ich ein a suchen wo der Grenzwert aller Funktionen 1/3 ist.
1/3·x^2 + 1/6·x - 1/6 = 1/3
x = - 3/2 ∨ x = 1
(x - 3)/(x^2 - x - 6) = 1/3
x = 1
Unter der Voraussetzung das die Funktion stetig sein soll würde ich also a = 1 setzen.
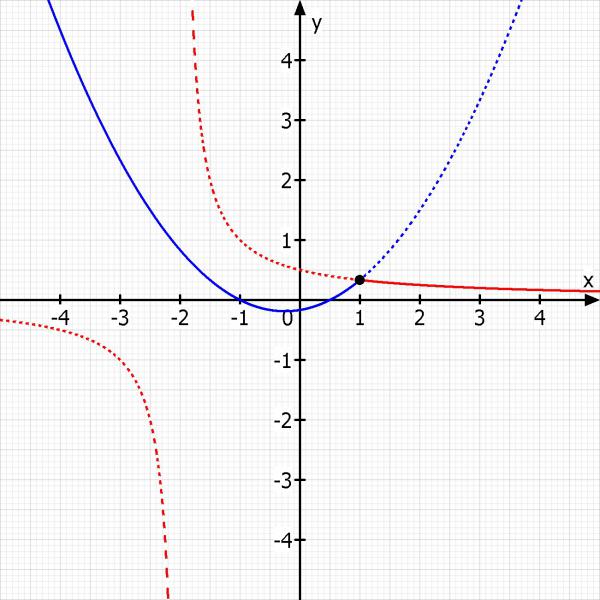
Ich mache noch eine Skizze. Hierbei ist eine Funktion nur im definierten Bereich durchgängig gezeichnet.