Für
Ra= 1/L ∫L0|y(x)|dx
musst du das bestimmte Integral von |y(x)| von 0 bis L berechnen und das Resultat durch die 'Länge' L dividieren.
Du erhältst den mittleren Abstand der Funktion y(x) von der x-Achse.
Bsp. y =0.1* x^3. L = 10.
Ra = 1/10 ∫100|0.1*x^3|dx |Betrag weglassen, da x^3 im Bereich [0,10]≥0
Ra = 1/100 ∫100 x^3 dx
= 1/100 * 1/4 x^4 |o10 = 1/400 * 10^4 - 0 = 25
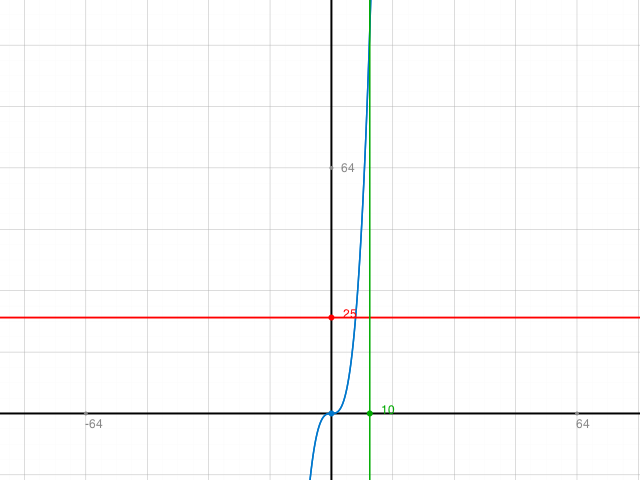
Skizze: Es sollte eigentlich so sein, dass die beiden Flächenabschnitte unter- resp. über der roten Linie gleich gross sind.