f(x) = e^{-x}·(-x + t + 1)
f'(x) = e^{-x}·(x - t - 2)
Extremstelle für
e^{-x}·(x - t - 2) = 0
x - t - 2 = 0
x = t + 2
t = x - 2
f(t + 2) = -e^{-t - 2}
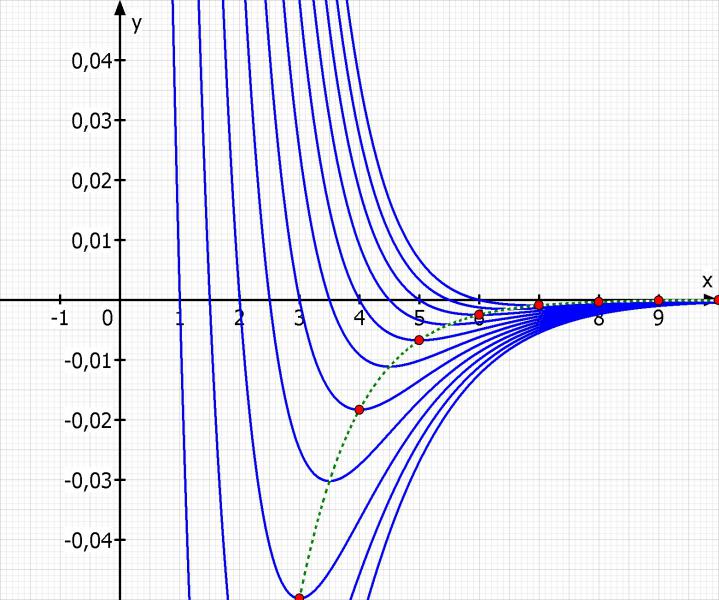
Laut Skizze sind das Tiefpunkte
Ortskrurve der Extrempunkte
f(x) = e^{-x}·(-x + t + 1) = e^{-x}·(-x + (x - 2) + 1) = -e^{-x}
Skizze: