Frage:
Gegeben sei f(x) \( =-x^{2}-x+2 . \) Die Tangente an den Graphen von \( f \) bei \( x=0 \) schließt mit den beiden Koordinatenachsen eine dreieckige Fläche ein. Der Graph von f teilt diese in zwei Stücke mit ihren Inhalten \( \mathrm{A}_{1} \) und \( \mathrm{A}_{2} \). Bestimmen Sie das Teilungsverhältnis \( \mathrm{A}_{1}: \mathrm{A}_{2} \)
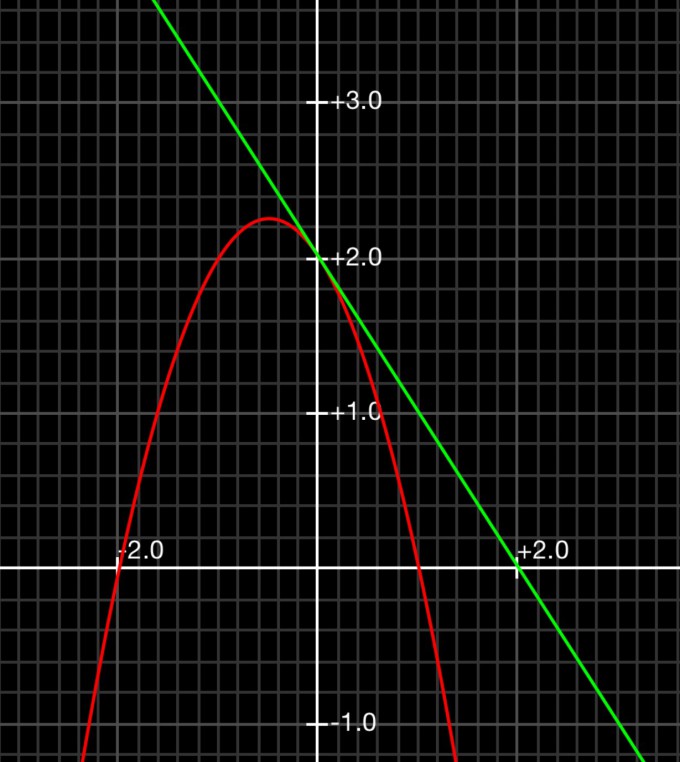
Skizze :Siehe Bild
Meine Rechnung:
Zuerst habe ich die gesamte Fläche gebildet, indem ich die Tangente an der stelle x=0 berechnet habe => t(x)=-x+2
Diese hat den Schnittpukt mit ser x-Achse bei 2, also liegt die obere Grenze des Integrals bei 2 und die untere bei 1.
Agesamt=1FE
Nun habe ich den Teil berechnet den die Funktion abschließt
A=7/6FE
Meine Frage wie funktioniert das mit den Teilungsverhältnis?
Ich habe diese Frage auch schon bei einer anderen Aufgabe von vor 1-2Stunden gestellt... Doppelt schadet natürlich nicht:)
Es ist wichtig, das ich dieses Problem langsam einmal löse...den wir rechnen absofort nur noch mit solchen Aufgaben und es bringt mich zur Verzweiflung.
Lg und vielen Dank schon im Voraus