Hallo ihr Lieben :) Ich war eine Doppelstunde krank, und verstehe jetzt das Thema nicht mehr / bzw. nicht so gut, deswegen konnte ich meine Hausaufgaben nur Ansatzweise erledigen. Manche Aufgaben konnte ich zwar, aber das Ergebnis sieht irgendwie falsch aus :( Kann mir da jemand helfen und mir die richtigen Lösugsweg zeigen?
Tut mir leid für die Mühe, es sind Aufgabe 6 und 7 (vollständig), das was ich selber wusste habe ich as Bildhochgeladen, vielleicht ist etwas davon richtig :) Liebe Grüße
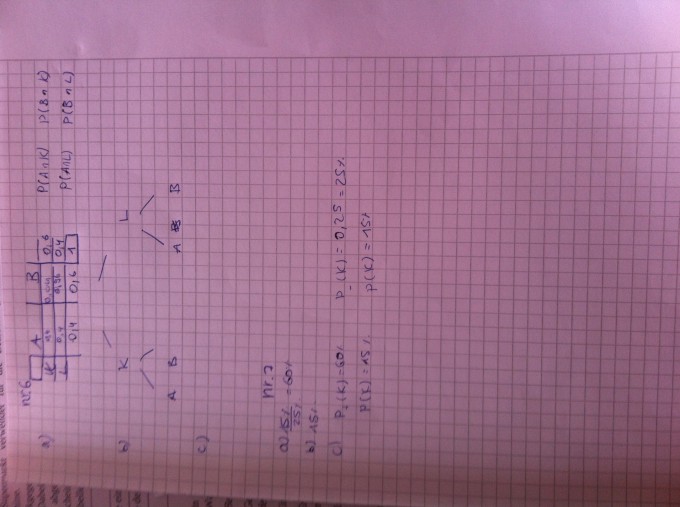
Aufgabe 6
a) Übersetzen Sie das nachstehende Baumdiagramm in eine Vierfeldertafel.
b) Konstruieren Sie ein zweites Baumdiagramm, das zur Vierfeldertafel passt.
c) Denken Sie sich einen Kontext aus, zu dem die Baumdiagramme passen könnten.
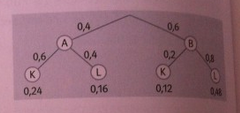
Aufgabe 7
Mithilfe von Tests versuchen Mediziner herauszufinden, ob eine bestimmte Erkrankung vorliegt: In der Sprache der Mediziner spricht dabei ein positives Testergebnis für das Vorliegen einer Erkrankung.
Lesen Sie aus der Vierfeldertafel ab, wie groß die Wahrscheinlichkeit ist, dass
a) ein Patient mit positivem Testergebnis tatsächlich krank ist,
b) er Test bei einem Kranken tatsächlich anschlägt (positiv ist).
Prüfen Sie die Gültigkeit der Ungleichungen P+(K) > P(K) bzw. P-(K) < P(K) und fassen Sie die Bedeutung dieser Ungleichungen in Worte.
Vierfeldertafel:
| K: krank
| G: gesund
|
|
Teset +
| 0,15
| 0,1
| 0,25
|
Test -
| 0,05
| 0,7
| 0,75
|
| 0,2
| 0,8
| 1
|
+ bedeutet: der Test schlägt an
- bedeutet: negatives Testergebnis
a)