die Aufgabe lautet: Untersuchen Sie die Reihen auf Konvergenz.
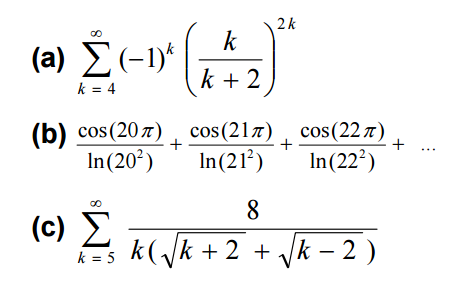
Meine Überlegung:
a) Das (-1)k gehört zu leibniz reihe, der rechte teil wird immer kleiner. Daher würde ich sagen, das die reihe gegen einen bestimmten punkt konvergiert.
b) diese reihe ist divergent, da man am anfang eine etwas größere postive zahl hat und dann eine etwas kleiner zahl abzieht. das heißt man addiert einfach die ganze zeit etwas dazu im prinzip, daher nicht endlich.
c) ist ganz klar divergent würde ich sagen, da 1/k divergent ist und das im prinzip auch das selbe ist.
natürlich geht es um mir um eure erklärung und wie man es mathematisch richtig schreibt.
MFG