a) f(x) = sin(x)
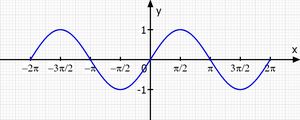
Mononon steigend im Bereich von (-pi/2 + 2k*pi) bis (pi/2 + 2k*pi)
Monoton fallend im Bereich von (pi/2 + 2k*pi) bis (3/2*pi + 2k*pi)
Konvek im Bereich (pi + 2k*pi) bis (2*pi + 2k*pi)
Konkav im Bereich (0 + 2k*pi) bis (pi + 2k*pi)
Diese Bereiche sind leicht abzulesen, wenn man sich die Funktion einmal wie oben skizziert. Wenn ein rechnerischer nachweis gebraucht ist hier die Bedingungen:
Monoton Steigend → f'(x) >= 0
Monoton Fallend → f'(x) <= 0
Konvex → f''(x) > 0
Konkav → f''(x) < 0
Probier vielleicht selber mal die rechnerischen Bedingungen zu prüfen.