Ich fange mal an mit
Wo in D max (f) ist f(x) streng monoton wachsend bzw. fallend ?
Hier ist zu bestimmen, wo f ' (x) > 0 resp. < 0 ist.
1. f(x)=( x^3)-(3x^2)+3x
f ' (x) = 3 x^2 - 6x + 3 = 3(x^2 - 2x + 1) = 3(x - 1)^2 immer ≥ 0. Somit monoton steigende Kurve 3. Grades
f '(x) = 0 für x = 1 Terrassenpunkt in T(1|0)
f(x) streng monoton steigend in M = {x| x Element R, x≠ 1}
2. f(x)= √(1 - x^2)
Das ist eine bekannte Funktionsgleichung. Ihr Graph ist die 'obere' Hälfte des Einheitskreises.
(Anm: Folgt direkt aus Pythagoras für P(x|y) auf Einheitskreis. x^2 + y^2 = 1^2 , y^2 = 1 - x^2. Für P(x|y) 'oberhalb' der x-Achse: y = √(1-x^2))
Hier weiss man ohne zu rechnen, dass Dmax = [-1,1] und dass f(x) in ]-1,0[ streng monoton wächst und in ]0,1[ streng monoton fällt.
Wo in D max (f) ist f(x) konvex bzw. konkav ?
Bei konvexen Kurven liegen alle Punkte der Kurve, die sich zwischen den Schnittstellen von Kurve und Sekante befinden, unterhalb der Sekanten, bei konkaven oberhalb. vgl. Abb. in Wikipedia: https://de.wikipedia.org/wiki/Konvexe_und_konkave_Funktionen
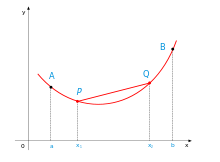
Sogenannte Linkskurven sind konvex, Rechtskurven konkav.
In Linkskurven ist die 2. Ableitung positiv in Rechtskurven negativ.
1. f(x)=( x^3)-(3x^2)+3x
Polynom 3. Grades mit f ' (x) = 3 x^2 - 6x + 3 somit
f '' (x) = 6x - 6 = 6 (x-1)
6 (x -1) ≥ 0 falls x ≥ 1. -----> f(x) konvex in [1, unendlich [
6 (x -1) ≤ 0 falls x ≤ 1. -----> f(x) konkav in ] - unendlich, 1]
2. f(x)= √(1 - x^2)
Graf ist in ganz Dmax konkav, Also in [-1,1]. (denn die obere Hälfte eines Halbkreises ist eine Rechtskurve )