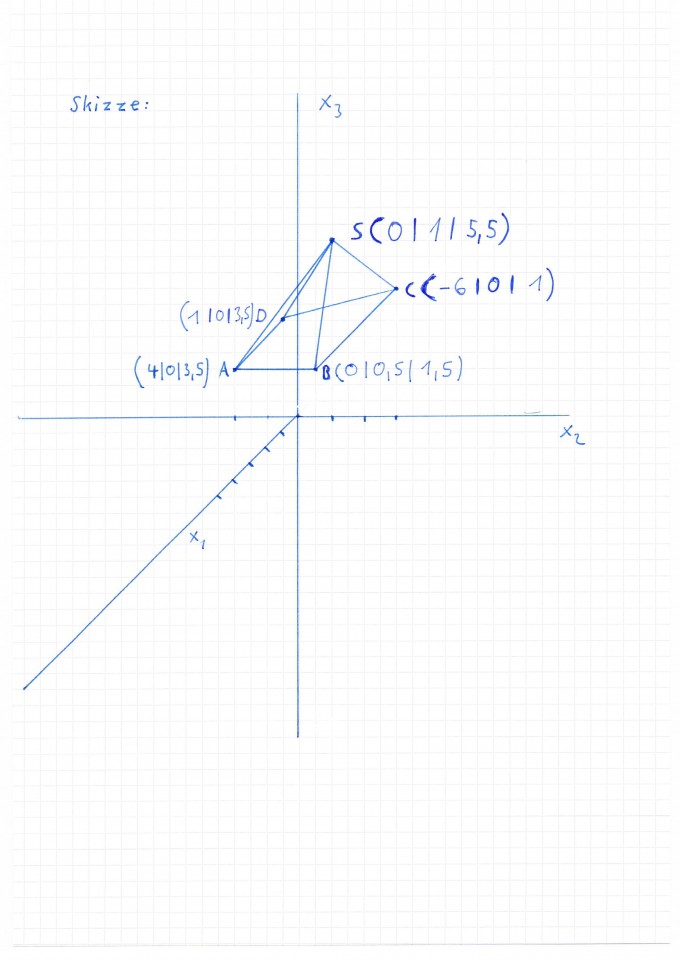
Ich übe gerade analytische Geometrie, weiß jemand wie ich bei einer Pyramide bei der jede Seite unterschiedlich lang ist, die Höhe berechnen kann ?
Die Pyramide hat die Grundseiten AB BC CD DA und die Spitze S.
Normalerweise habe ich die Höhe immer so ermittelt, indem ich die Kantenlänge z.B. AS bestimmt habe.
Dann die Diagonale der Grundfläche durch zwei teilte und dann die Höhe mit dem Satz des Pythagoras ermittelte. Jetzt sind hier viele Seiten unterschiedlich lang und es müsste auch zwei verschieden lange Diagonalen geben. Hat jemand eine Idee, wie ich die Höhe der Pyramide hier am einfachsten berechnen kann ?