Hochpunkte cos(x)*cos(2x)

Question

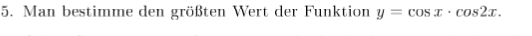
Mein erster Gedanke war die Funktion mit Additionstheoreme und trigonome. Pythagoras umzuformen.

Ich komme auf die Funktion y = cosx(2cos^2(x)-1), die so auch stimmt.

Jedoch muss ich ja die Produktregel anwenden und die Ableitung = 0 setzen um auf Extrempunkte zu kommen.

Da die Ableitung ziemlich komplex ist und laut Taschenrechner es mehrere Lösungen gibt, glaube ich das ich auf dem falschen Weg bin. Aber in der Aufgabe ist ja die Rede von einem größten Wert und nicht mehrere..

Answer 1

Naja. cos(x) ist im bereich ± 1 und cos(2x) ist auch im bereich ± 1

Sicher gibt es ein Maximum wenn beide 1 werden was sicher bei x = 0 der Fall ist.

So kannst du eigentlich selber leicht herleiten das die Maxima den Funktionswert 1 haben und bei 0 + k*2*pi liegen und die Minima den Funktionswert -1 haben und bei pi + k*2*pi liegen.

Answer 2

Ziel der Aufgabe ist es den maximalen Wert der Funktion zu finden, also das globale Maximum.

Im besten Fall wird cos(x)*cos(2x) eins sein, da beide Faktoren maximal 1 werden können. Dieses Maximum wird für x=0 auch angenommen.

--> y_max=1