Medikament mit Stärke R(r,s) = (2r+s)e^{-r^2-s}. Wie sind r und s für eine maximale Wirkung zu wählen?

Question

Ein Medikament mit zwei Wirkungsbestandteilen soll so eingestellt werden, dass die Wirkung maximal wird. Die Stärke R der Wirkung lässt sich durch die funktionale Abhängigkeit

R(r,s) = (2r+s)e^{-r^2-s}

beschreiben, dabei sind r bzw. s die Mengen der beiden Bestandteile. Wie sollte man r und s wählen, damit man maximale Wirkung erhält?

Comments

Bilde mal die partiellen Ableitungen und bestimme deren Nullstellen. Dann sehen wir weiter.

Answer 1

R(r, s) = e^{- r^2 - s}·(2·r + s)

dR / dr = - 2·e^{- r^2 - s}·(2·r^2 + r·s - 1)

dR / ds = - e^{- r^2 - s}·(2·r + s - 1)

Ich setzte die Partiellen Ableitungen 0

2·r^2 + r·s - 1 = 0
2·r + s - 1 = 0

Diesen Gleichungssystem hat die Lösung r = 1 ∧ s = -1.

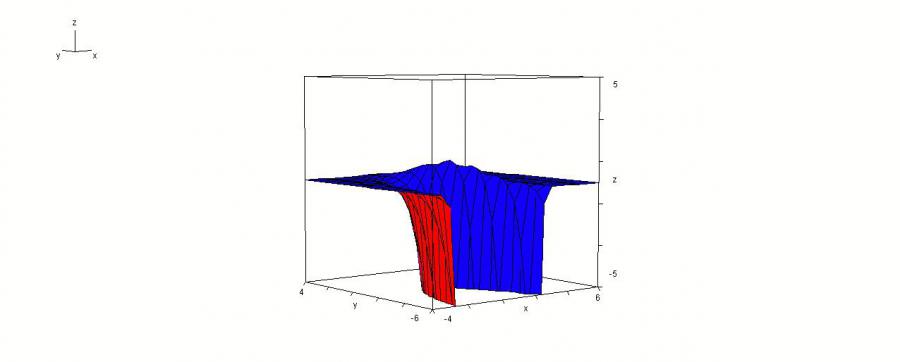
Ich mache mal eine Skizze. Hier kann man den Hochpunkt sehen.

Comments

als Ergebnis habe ich auch r =1 und s = -1 heraus. Bloß was bedeutet das Ergebnis
im Sachzusammenhang ?

  mfg Georg

---

Das eine negative Menge s genommen werden muss :-)

Hier ist es wohl so das wir s = 0 setzen müssen. Dann wäre r = √0.5.

Mehr über den Sachzusammenhang geht aber aus der Aufgabe nicht hervor.