zu welchen Zeiten ist Auslenkung dem Betrag nach gleich halbe Amplitude?

Question

periodendauer ist 0.12s

x=xm *sin(wt)

mein versuch:

also die nullstellen der funktion liegen bei 0s,0.06s und 0.12s

dann liegt das eine maxima bei 0.03s und das andere bei 0.09s

dann ist die halbe amplitude in der ersten periode bei 0.015s,0.045s,0.075s und 0.11s ?

Answer 1

mit den Extrema kann man hier nicht arbeiten, weil die gesuchten t-Werte nicht in der Mitte zwischen Extremum und Nullstelle liegen.

ω = 2π / T = 2π / 0,12s  = 50π/3  s^-1

x = x_m • sin(ωt) = x_m • sin( 50π/3 s^-1 · t ) = ±1/2 x_m  | : x_m

sin(  50π/3 s^-1 · t ) = ±1/2

sin(u) = ± 1/2 hat die die Lösungen

u = π/6 + k·2π  oder u = 5/6·π/ + k·2π oder u = 7π/6 + k·2π oder u = 11π/6 + k·2π

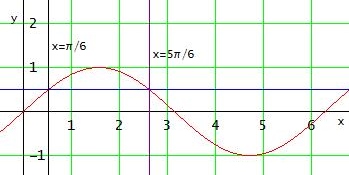
Mit k ∈ ℤ

 50π/3s^-1 · t  = π/6 + k · 2π  oder   50π/3s^-1 · t  = 5π/6 + k · 2π                | : 50π/3 s^-1

 oder  50π/3 s^-1 · t  = 7π/6 + k · 2π  oder   50π/3 s^-1 · t  = 11π/6 + k · 2π   | : 50π/3  s^-1  

t  = (1/100 + 3k / 25) s   oder   t = (5/100 + 3k / 25) s    mit  [ k ∈ ℤ ]

t  = (7/100 + 3k / 25) s   oder   t = (11/100 + 3k / 25) s    mit  [ k ∈ ℤ ]

Für k = 0 ergibt sich z.B.  t₁ = 0,01 s ; t₂ = 0,05 s  ;   t₃ = 0,07 s  ;  t₄ = 0,11 s

Gruß Wolfgang