Tangente bestimmen die durch einen Punkt geht und durch den Graphen von y=4-1/2 x²

Question

Die Aufgabe lautet wie folgt:“ Die Mittellinie der gezeichneten Rennstrecke wird durch y=4-1/2x² beschrieben. Bei spiegelglatter Fahrbahn rutscht ein Fahrzeug und landet im Punkt Y(0/6). Wo hat das Fahrzeug die Straße verlassen.“

Hier muss man ja die Tangenten bestimmen die durch Y(0/6) gehen. Dabei komm ich aber auf komische Ergebnisse, könnt ihr mir weiterhelfen?

Comments

Kannst du schon Ableitungen bestimmen oder behandelt ihr diese Frage beim Thema quadratische Funktionen?

---

12 Klasse also Ableitungen kennen wir schon.

Answer 1

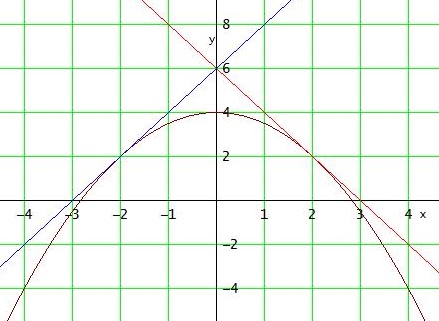
f(x) = - 1/2 * x² + 4

f '(x) = -x           [ ohne f ' vgl unten ]

Gesucht ist der Berührpunkt B(u|f(u)) der Tangente an G_f , die durch P(0|6) verläuft.

Die Gerade durch den Punkt P( x_p | y_p ) mit der Steigung m hat die Gleichung

y = m • ( x - x_p ) + y_p            [ Punkt-Steigungs-Formel ]   

Gleichung der Tangente t:   y = f '(u) * (x - 0) + 6

Setzt man die Koordinaten von B in t ein, hat man

     f(u)  = f '(u) * u + 6

      - 1/2 * u² + 4  = - u² + 6  →  u = ± 2

   →  In B(2 | f(2) ) =  B₁(2/2) oder B₂(-2|2)    verlässt das Fahrzeug die Straße 

         (je nachdem aus welcher Richtung es kommt)

--------------

ohne f '(x)

Die Tangente hat die Gleichung  y = m * x + 6   [Achsenabschnitt = 6 wegen P]

Der Berührpunkt P ist die einzige Schnittstelle mit f:

- 1/2 * x² + 4 = m * x + 6

Umstellen und pq-Formel anwenden ergibt:

x₁ = - √(m² - 4) - m   ;   x₂ = √(m² - 4) - m

die Wurzel muss gleich 0 sein, weil es nur eine Schnittstelle gibt

→  m² = 4  →  m = ±2  ( bei -2 fährt das Fahrzeug in die andere Richtung )

→  x₁ = -2  ; x₂ = 2

weiter wie oben

 Gruß Wolfgang

Comments

Vielen Dank, jetzt versteh ichs.