Gleichung für Kreisfunktion lösen..

Question

ich habe 2 Punkte: "P1" und "P2". Für P2 gibt es außerdem eine Steigung "t", die orthogonal zu der Steigung der Funktion an der Stelle ist.

P1_x = 0;   P1_y = r

P2_x = x;   P2_{y =} P1_y - r_y

Gesucht sind r und f für eine Funktion nach dem Schema   r - r_y = sqrt( r² - (f * x)² )

Die Funktion soll beide Punkte berühren, bei P1 eine Steigung von 0 und bei P2 eine Steigung orthogonal zu t haben. rausgefunden habe ich, dass   f = sqrt( (Py / t) / Px )

Beispielsweise könnte nun für r_y = 2, für x = 8 und für t 1 gegeben sein.

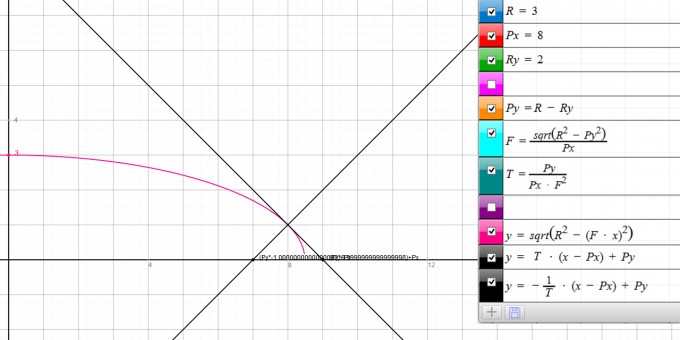
Ich hänge ein Bild der Funktion an, wie sie für dieses Beispiel aussehen sollte. Die Werte dafür habe ich erhalten, indem ich r = 3 gesetzt und den Rest entnommen habe.

Comments

> eine Funktion nach dem Schema   r - r_y = sqrt( r² - (f * x)² )

Das ist keine Funktion.

---

Ich nehme an weil es kein y hat? Wird dann wohl eine Gleichung sein.

Kann den Text nicht bearbeiten. Ändert ja aber auch nichts an den Umständen.

---

Als Gleichung betrachtet kann man sie einfach nach r umstellen und so eine Formel bekommen, mit der man aus einem vorgegebenen Wert für f einen Wert für r berechnen kann.

Mir ist nicht ganz klar, welche Rolle die Funktion spielen soll, von der mehrfach die Rede ist. Augenscheinlich ist die Funktion so unwichtig, dass sie noch nicht ein mal einen Namen hat. Auch der Wert von t spielt bei der Lösung der Gleichung keine Rolle.

---

Man hat ja eben keinen festen Wert für f. Nur für t. Aus t kann ich ein f berechnen. Allerdings berücksichtigt diese Rechnung nicht, dass r = P1_y sein muss.
Es gibt aber nur die eine Möglichkeit für r und f um durch die Funktion y = sqrt(r^2 - (f * x)^2) den Graphen des Bildes zu erhalten.
"t" ist die Steigung des Punktes der Funktion y = sqrt(r^2 - (f * x)^2.
Auf dem Bild sind 2 schwarze Linien. Der Schnittpunkt der beiden ist P( r - r_y | x ). Rechts auf dem Bild sieht man noch die funktionen für die Schwarzen Linien.

---

> Man hat ja eben keinen festen Wert für f

Natürlich nicht. Deshalb ja auch die Aufgabe "Gesucht sind r und f".

> Aus t kann ich ein f berechnen

Welche Aussage in der Aufgabenstellung stellt einen Zusammenhang zwischen t und f her?

---

>Welche Aussage in der Aufgabenstellung stellt einen Zusammenhang zwischen t und f her?

Ein Kriterium ist ja das der Graph an Stelle P2 die Steigung  -1/t  hat. Einfluss auf t haben r und f. Dadurch entsteht ein zusammenhang zwischen t und f.