Erst mal sauber {syntaktisch richtig} aufschreiben:
log(x)/log(3)+log(7*(x+3))/log(2)=3
Dabei nie Klammern weglassen, da sie für Funktionen wichtig sind!
Dann schauen, ob sie per LambertW Funktion lösbar ist:
http://www.lamprechts.de/gerd/LambertW-Beispiele.html
Passt leider sie nicht in eine der Formen §1 ... §8,
also numerisch.
Neben Bisektion und Newton-Verfahren funktioniert hier das viel einfachere Verfahren der selbstkonvergierenden Iteration. Mit anderen Worten: nach x umstellen und das Ergebnis der Funktion immer wieder neu in die Formel einsetzen:
log(x)/log(3)=3-log(7*(x+3))/log(2) | *log(3)
log(x)=(3-log(7*(x+3))/log(2))*log(3) | e^x
x= e^[(3-log((x+3)*7)/log(2))*log(3)] = exp((3-log((x+3)*7)/log(2))*log(3))
Der Iterationsrechner zeigt das selbstkonvergierende Verhalten -> also die Konvergenz gegen Grenzwert:
http://www.gerdlamprecht.de/Roemisch_JAVA.htm#exp((3-log((x+3)*7)/log(2))*log(3))@N@B0]=0.2;@N@Bi+1]=Fx(@Bi]);@Ni%3E8@N0@N0@N#
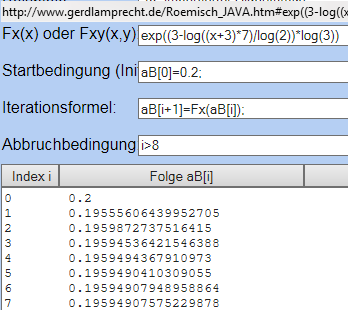
Bei Interesse kann ich die beiden anderen Verfahren auch zeigen
(Beispiele 2 & 118 anpassen)